L’homogénéité dans un modèle bâlois : la quadrature du cercle ?
Réflexions et propositions pour une convergence des exigences réglementaires et des pratiques opérationnelles
Juillet 2023
Auteur
Olivier Gassner
Relecteurs
Éric Bataille
Alicia Gardette
Sommaire exécutif
L’objectif de cette publication est de questionner la place de l’homogénéité des échelons de notation dans un dispositif bâlois, ainsi que les modalités de contrôle de celle-ci. Notre ambition sera de proposer une aide au diagnostic des difficultés rencontrées par l’industrie bancaire en la matière et d’avancer plusieurs propositions visant la convergence entre exigences réglementaires et contraintes opérationnelles. Notre propos visera à recentrer le débat sur le rôle de l’homogénéité des classes dans un dispositif bâlois, en explicitant les conséquences d’un manque d’homogénéité sur la précision des mesures de risque de crédit. Nous tenterons de mettre en évidence l’incohérence existant entre les pratiques de place en matière de contrôles et le rôle de l’homogénéité, en défendant la thèse que celle-ci ne se résume pas à un problème statistique, mais adresse également la gouvernance des modèles, tout comme leur méthodologie de développement et de revue.
Après une brève introduction au formalisme bâlois, nous montrerons que l’approche ASFR ne saurait contribuer à une mesure prudente du risque de crédit en l’absence d’homogénéité des classes de risque sur lesquelles les paramètres bâlois sont appliqués. Nous explorerons différentes causes d’hétérogénéité caractérisant un portefeuille de crédit. Ainsi, nous nous intéresserons à la variété des typologies de contrats, la dynamique de cette variété, ainsi qu’à la finesse avec laquelle celle-ci est appréhendée, soit la granularité de la segmentation du portefeuille. Une fois les causes identifiées, nous en expliciterons les conséquences d’un point de vue prudentiel, tant au niveau du segment de calibrage que du portefeuille lui-même. En particulier, nous mettrons en évidence le risque d’introduire un biais dans la mesure du risque de long-terme.
Une seconde partie sera dédiée aux dispositifs de contrôle et de compensation observés dans l’industrie. En particulier, nous décrirons comment des marges de conservatisme peuvent être calibrées afin de palier un défaut d’homogénéité, ou comment la définition de plusieurs segments de calibrages, voire plusieurs fonctions de score peuvent adresser l’hétérogénéité du portefeuille. Puis nous introduirons les trois niveaux de contrôle nécessaires à l’évaluation de l’homogénéité des classes : statistique, méthodologique et gouvernance. Le premier, plus intuitif, renvoie au contrôle des niveaux de risques observés au sein du portefeuille, le plus souvent à l’aide de méthodes inférentielles. Cependant, la multiplicité des critères de conformité requiert une méthodologie de contrôle explicite assurant la hiérarchie d’indicateurs statistiques parfois contradictoires. Enfin, la place et la récurrence de ces contrôles renvoient à la gouvernance des modèles, tout comme le degré de contrainte que ces contrôles font peser sur le dispositif. Force est de constater que les différentes parties prenantes n’accordent pas la même attention à ces trois niveaux. En effet, seules les exigences en matière de gouvernance de modèle sont clairement posées par le régulateur, alors que les institutions bancaires tendent à se concentrer principalement sur le niveau statistique.
Dans la dernière partie de notre article, nous proposerons une critique de l’efficacité des pratiques de place quant au contrôle de l’homogénéité. Nous dresserons un constat d’échec de ces pratiques, en posant le diagnostic d’une recherche de critères souvent contradictoires. Aussi, nous montrerons la nécessité de considérer la vie du portefeuille et du modèle dans le choix et l’importance des indicateurs statistiques. Par ailleurs, nous proposerons plusieurs pistes d’investigation pouvant être explorées, en soulignant le manque de marges de manœuvres à disposition des institutions bancaires, piégées dans une approche purement statistique du superviseur et un positionnement flou du régulateur. En particulier, nous proposerons de compléter cette vision par une dimension méthodologique, en redéfinissant clairement la place de l’homogénéité dans la réglementation bâloise, complétant les indicateurs quantitatifs par des évaluations qualitatives des mécanismes de contrôle auxiliaires tels que le backtesting, ainsi que par l’introduction d’indicateurs de stabilité, de matérialité et de complexité opérationnelle.
Nous ouvrirons enfin la discussion sur l’apport des méthodes de Machine Learning, en posant la question de l’homogénéité comme celle de la performance prédictive des scores. A date, ces méthodes sont loin de représenter la solution idoine, et le développement d’une heuristique nouvelle fondée sur le concept d’homogénéité nous semble nécessaire. Leur paramétrage complexe propose de nombreux défis en matière de gouvernance et de supervision. Cette problématique, à l’instar du risque climatique, constituera l’un des grands chantiers des acteurs du risque de crédit.
Introduction
Le programme IRB Repair lancé en 2016 par l’Autorité Bancaire Européenne (EBA) pose un nouveau cadre d’analyse en matière de modélisation du risque de crédit. Afin de se conformer à ces nouvelles exigences, les institutions supervisées ont dû adapter leurs dispositifs de notation, en s’appuyant notamment sur les « Orientations sur les estimations de probabilité de défaut (PD), les estimations de perte en cas de défaut (LGD) et sur le traitement des expositions sur lesquelles il y a eu défaut 01, ci-après notées GL EBA. Le retour d’expérience du secteur permet aujourd’hui de dresser le bilan de l’intégration de ces nouvelles règles par l’industrie bancaire. En particulier, nous pouvons noter que la notion d’homogénéité des classes de notation revient régulièrement comme une préoccupation majeure du superviseur. Force est de constater que les institutions bancaires peinent à satisfaire aux exigences de celui-ci en la matière.
Nous proposerons dans un premier temps un bref rappel théorique sur le modèle ASRF, où nous introduirons les éléments analytiques sollicités au cours de cet article. Nous soulignerons en particulier les limites de ce modèle, ainsi que l’importance d’une segmentation du portefeuille de crédit en échelons de notations homogènes au regard du risque. Nous tenterons ensuite d’analyser les causes et conséquences d’un défaut d’homogénéité, tant au niveau du segment de calibrage qu’à celui du portefeuille.
Une seconde partie sera dédiée aux dispositifs de contrôle et de compensation. En particulier, nous verrons comment une approche conservatrice peut pallier un défaut d’homogénéité. Puis nous aborderons les questions méthodologiques ainsi que les éléments de gouvernance que nous jugeons nécessaires à une bonne appréhension de la notion d’homogénéité. Nous témoignerons de certaines pratiques de place en matière de contrôle de l’homogénéité des échelons de notation, ainsi que les exigences réglementaires.
Dans la dernière partie de cet article, nous proposerons une lecture critique de ces pratiques de place, mettant en évidence certaines de leurs faiblesses conceptuelles. En particulier, nous verrons comment la recherche de critères de conformité contradictoires peut nous éloigner d’un mécanisme de contrôle performant et opérationnel. Nous discuterons enfin de l’apport des méthodes de Machine Learning dans la quête d’homogénéité.
L’homogénéité dans un dispositif bâlois
Rappels sur le modèle de Vasicek, l’approche ASRF, et la formule de Bâle
L’objectif des modèles IRBA est de prévoir les pertes inattendues (UL) relatives à un portefeuille, qui représentent les pertes économiques potentielles liées au risque de crédit au regard d’un niveau de risque inattendu. Les accords de Bâle exigent que les institutions bancaires couvrent ces risques par leurs fonds propres (Capital Réglementaire). C’est dans ce contexte IRBA que nous nous placerons, retenant le cadre méthodologique proposé par les GL EBA.
Celui-ci s’inspire du modèle de valorisation des actifs financiers proposé par Merton (1974) 02 et repris par Vasicek (2002) 03 et Gordy (2003) 04. D’après celui-ci, la valeur de l’actif est définie selon deux composantes, mesurant les facteurs systématiques (communs à toutes les contreparties) et idiosyncratiques (spécifiques à une contrepartie). Le Comité de Bâle a retenu cette formalisation, en y introduisant plusieurs hypothèses, comme l’absence de corrélation entre les différentes contreparties 05 du portefeuille, l’hypothèse de granularité infinie, l’existence d’un facteur de corrélation unique aux facteurs systémiques, ou le choix d’un horizon de prévision fixé à 12 mois.
Ce modèle ajusté définit le modèle ASRF (Asymptotic Single Risk Factor), dans lequel le risque de défaut est exprimé en fonction d’un facteur unique, la Probabilité de Défaut (PD). Celle-ci dépend des facteurs systématiques et mesure le niveau de risque moyen de long-terme (non-conditionnel) et sert de base au calcul du risque inattendu (conditionnel). Les formules de la PD conditionnelle et des actifs pondérés (RWA) sont introduites dans la Capital Requirements Regulation (CRR) 06. Pour plus de détails, nous suggérons la démonstration concise de Genest et Brie (2013) 07.
Les hypothèses et limites du modèle Bâlois et la place de l’homogénéité
Nous l’avons vu, le modèle ASRF ne considère que les facteurs systématiques. Aussi, afin d’adresser l’hétérogénéité de leur portefeuille en matière de risque, les institutions sont encouragées à définir une échelle de notation, où chaque échelon de l’échelle se voit attribuer un estimateur de la PD spécifique. La position d’une contrepartie sur l’échelle est conditionnelle à ses facteurs idiosyncratiques.
Cette exigence constitue un point crucial dans l’estimation du risque lié au portefeuille dans la mesure où les contreparties regroupées dans le même échelon doivent présenter une certaine homogénéité en matière de risque de long terme. Nous retrouvons d’ailleurs cette notion d’homogénéité dans deux articles du CRR repris dans les GL EBA :
- L’article 142 du CRR (Définitions) définit un type d’exposition comme « un groupe d’expositions géré de manière homogène». Cette notion renvoie à l’application de processus ou de méthodes similaires pour un même type, mais potentiellement différents pour d’autres types.
- L’article 170 3, c) du CRR (Structure des systèmes de notation) précise que « le processus d’affectation des expositions aux échelons ou catégories prévoit une différenciation adéquate des risques, leur regroupement en ensembles suffisamment homogènes et permet une estimation précise et cohérente des caractéristiques des pertes au niveau de chaque échelon ou catégorie».
- L’article 69 des GL EBA (Homogénéité des échelons ou catégories de débiteurs) indique que « les établissements devraient vérifier l’homogénéité des débiteurs ou des expositions affectés aux mêmes échelons ou catégories », afin que « chaque débiteur affecté à un échelon ou une catégorie présente un risque de défaut raisonnablement similaire » et que « soient évités les chevauchements significatifs de distributions du risque de défaut entre échelons ou catégories »
- Enfin, l’article 130 des GL EBA (Homogénéité des échelons ou catégories de facilité de crédit) transpose ces exigences sur le paramètre LGD.
Nous constatons que la notion d’homogénéité porte autant sur les processus et méthodes que sur la précision statistique des estimateurs du paramètre de risque. En définitive, le cadre méthodologique prévu par le modèle ASRF repose sur une hypothèse sous-jacente d’homogénéité des échelons de notation. Ces échelons sont d’ailleurs appelés « classe homogène de risque ». Dès lors, la mise en place de mécanismes de contrôle revêt une importance cruciale, car en l’absence d’homogénéité, la formule de Bâle ne fonctionne pas, et son application peut mener à une constitution de capital réglementaire insuffisante. C’est ce que nous proposons d’explorer dans les sections suivantes.
Les causes d’hétérogénéité
La typologie des contreparties et leur dynamique
Les portefeuilles de crédit, qu’ils soient Retail, Corporate, Souverains, etc., regroupent des typologies de contrats différentes, dont les caractéristiques peuvent être sources d’hétérogénéité. Au-delà de ces différences statiques, la composition du portefeuille au cours du temps est un facteur d’instabilité affectant la précision des estimateurs bâlois. Aussi, l’évolution des volumétries, la sensibilité des contreparties aux conditions économiques, leur propre dynamique de risque, et le cadre juridique sur les différents actifs financiers doivent être pris en compte afin d’assurer une estimation précise du risque. En conséquence, un modèle de discrimination (ex : score comportemental) performant est indispensable à la construction d’une segmentation homogène du portefeuille08. Par voie de conséquence, la représentativité de l’échantillon historique au portefeuille d’application est un facteur d’homogénéité qu’il convient de contrôler, tant pour la discrimination du risque, que pour sa quantification.
La granularité de la segmentation
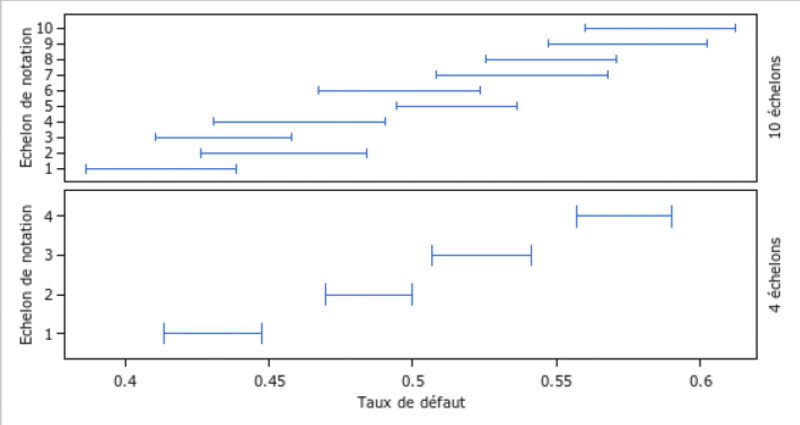
Aussi, la granularité de la segmentation, qui renvoie au nombre d’échelons composant l’échelle de notation, est l’un des aspects les plus ambivalents de l’homogénéité. Nous parlerons d’une granularité forte lorsque celle-ci résulte d’un nombre de classes élevé, et faible dans le cas inverse. La difficulté à trouver un équilibre entre granularités fortes et faibles peut être illustrée par la segmentation d’une échelle de score continue. Le graphique ci-dessous représente deux segmentations concurrentes de la même échelle de score, sur le même échantillon, en 4 ou 10 échelons. Les segments décrivent les intervalles de confiance à 95 % autour du taux de défaut moyen de chaque classe.
Nous constatons qu’une granularité forte maximise les chances de regrouper des individus comparables au regard du niveau de risque, mais augmente le risque de voir apparaitre des chevauchements significatifs des distributions de risque. Nous pouvons associer ce risque à la notion d’homogénéité inter classes. A l’inverse, une faible granularité limite les chevauchements, par l’épaisseur des tranches de risque ainsi créées, mais tend à regrouper des individus aux profils plus divers. Nous pouvons associer ce risque à la notion d’homogénéité intra classe.
Les conséquences d’un manque d’homogénéité
Le segment de calibrage
Le principe même de la segmentation du portefeuille est d’adresser l’hétérogénéité de celui-ci. Nous pouvons alors nous demander quelles seraient les conséquences d’un manque significatif d’homogénéité sur l’efficacité du dispositif de notation. Nous proposons de l’illustrer avec l’exemple d’une classe de notation unique.
La moyenne de long terme (LRA) mesure le risque moyen d’une classe sur un historique suffisamment long pour couvrir des périodes d’expansion et de récession économiques. Ainsi, même s’il existe plusieurs sous-populations aux niveaux de risque différents, la LRA représentera le niveau de risque moyen, de telle sorte que la sous-estimation du risque sur une sous-population sera compensée par la surestimation du risque sur l’autre sous-population. Nous serions tentés de penser que cela n’impacte pas la précision du calibrage des paramètres de risque. En effet, par construction, la LRA mesurée sur l’ensemble du portefeuille est égale à la moyenne pondérée des LRA mesurées sur chaque classe.
Cependant, le niveau de risque calibré par la LRA reste précis tant que la pondération des sous-populations reste stable. Aussi, si la structure du portefeuille varie au cours temps, notamment entre la période d’estimation et la période d’application, la LRA s’éloignera du risque moyen (pondéré) du portefeuille, et l’estimation du risque deviendra imprécise.
La présence de sous-populations aux dynamiques divergentes est donc de nature à créer des fluctuations du risque mesuré de façon ponctuelle autour de sa moyenne de long-terme. Aussi, la présence d’hétérogénéité dans une classe de notation provoque une plus grande volatilité des estimateurs, et, par voie de conséquence, peut mener à une sous-estimation du capital réglementaire dérivé du modèle ASRF. C’est la raison même de la définition d’échelons dans un segment de calibrage en classes de risque. Précisons que dans le cas où ces populations sont identifiées par le modèle, ces fluctuations se traduiront par des migrations entre les classes de risque, dont les pondérations ajustées des migrations permettent de conserver une mesure précise du risque 09.
Le portefeuille
Nous l’avons vu, la prise en compte des caractéristiques de risque est un facteur renvoyant à la typologie des expositions, et peut inciter à définir des segments de calibrage, voire des modèles de discrimination différents. En effet, une forte dynamique des sous-populations peut agir sur la précision des scores, dont les paramètres sont estimés au regard d’une population de modélisation dont la structure a pu changer avec le temps. Par extension, une dégradation de la performance d’un score altère sa capacité à considérer les facteurs idiosyncratiques du risque, et donc à ventiler les contreparties dans les différentes classes de risque du segment de calibrage.
Les mécanismes de compensation : de l’approche conservatrice
Comment certaines de ces causes sont déjà adressées par les marges de conservatisme
Les marges de conservatisme (MoC) introduites par les GL EBA couvrent les déficiences des systèmes de notation utilisés pour le calcul des fonds propres réglementaires selon 3 catégories. La catégorie A renvoie aux déficiences du système d’information et aux méthodologies d’estimation des paramètres. La catégorie B renvoie aux évolutions réglementaires, commerciales ou organisationnelles des institutions, qui peuvent remettre en cause la cohérence de l’historique de données. Enfin, la catégorie C porte sur l’erreur statistique liée à toute estimation, reprenant le concept d’intervalle de confiance. Dans la pratique, ces marges permettent d’adresser une large partie des conséquences d’un manque d’homogénéité des classes de notation.
Par exemple, la typologie des contrats, les évolutions du portefeuille liées à des changements dans la politique commerciale, la gestion du risque, ou des évolutions juridiques peuvent être adressés au travers de la marge de catégorie B, en vertu de l’article 37 des GL de l’EBA. Le même article autorise à palier certaines défaillances de modèle par une marge de catégorie A. L’interprétation d’un manque d’homogénéité en tant qu’une défaillance de modèle réalisant un biais systématique et matériel peut justifier l’ajustement de ce type de marge 10.
Prenons l’exemple d’une classe de risque regroupant des populations potentiellement hétérogènes. La simulation de différentes pondérations de ces populations, via l’utilisation des méthodes de Monte Carlo ou de l’approche Bootstrap, permet une mesure de la volatilité de la LRA calibrée sur cette classe, toutes choses étant égales par ailleurs. Nous pouvons alors construire un intervalle de confiance autour de la LRA, servant d’étalon à une MoC. Nous détaillons la méthodologie de calibrage de cette MoC dans l’encadré 1 ci-contre. La matérialité de cette incertitude peut être évaluée par une étude d’impact en RWA 11.
Nous avons vu que les dynamiques de sous-populations se reflètent dans la volatilité des taux de risque dans le cas où elles ne sont pas captées par le modèle sous-jacent. In fine, ces fluctuations impactent la variance de la LRA et seront susceptibles d’accroitre la marge de catégorie C (Art. 43 GL EBA). Par ailleurs, la variance de la LRA est sensible au niveau de granularité de la segmentation. Comme nous l’avons vu, celle-ci s’accroit à mesure que la granularité augmente.
Les dispositifs complémentaires
Cela étant dit, les MoC sont par essence temporaires, palliant une déficience censée être corrigée dans un intervalle de temps raisonnable. Aussi, d’autres dispositifs peuvent être indiqués lorsqu’il s’agit d’adresser des causes structurelles d’hétérogénéité. Par exemple, nous avons vu que la segmentation de l’échelle de notation visait à adresser l’hétérogénéité structurelle du portefeuille. Dans les cas de grande variabilité de profils de risque, il peut être envisagé de construire plusieurs scores ou plusieurs segments de calibrage, spécifiques à des sous-populations, voire plusieurs systèmes de notation. La nature transitoire ou structurelle de l’hétérogénéité du portefeuille peut être évaluée au travers d’études sur le portefeuille historique, ou des exercices de backtesting.
Soit une classe de risque d’effectif n admettant deux populations d’effectifs notés n1 et n2, tel que n1 + n2 = n, et p la probabilité pour une observation d’appartenir à la population 1. Supposons cette population plus risquée tel que LRA1 > LRA2. Ainsi, n1 suit une loi Binomiale de paramètres p et n, tel que :
Le poids w1 de la population 1 dans la classe de risque est donc une variable aléatoire définie sur l’intervalle [0;1], tel que :
Nous pouvons définir un intervalle de confiance autour du poids moyen de la population 1 comme suit :
Où p̂ est un estimateur sans biais de p. La LRA de la classe est calculée comme la moyenne des LRA calibrée sur chaque population pondérée par leur poids. Nous pouvons donc définir une LRA « dégradée » en substituant le poids de la population la plus risquée par la borne supérieure de l’intervalle de confiance construit autour de son estimateur, comme suit :
LRA* = ICsup LRA1 + (1 – ICsup)LRA2
Et de déduire une MoC calibrée comme la différence entre la LRA de la classe et sa version « dégradée ». Ajoutons que dans les cas où les hypothèses sous-jacentes de distributions seraient remises en cause, l’estimation de V(w1), voire de ICsup , peut être réalisée en appliquant des méthodes de rééchantillonnage.
Encadré 1 : Proposition méthodologique pour le calibrage d’une MoC
Le contrôle des causes d’hétérogénéité
Gouvernance, méthodologie, et statistique
Nous avons vu que la notion d’homogénéité ne se réduisait pas à des variations de taux de défaut ou de perte, mais adressait également la structure du portefeuille et sa dynamique, en matière de typologie de contrat, ou tout autre facteur associé au risque. Par ailleurs, nous avons mis en évidence l’antagonisme entre les homogénéités inter et intra classe résultant de la granularité de la segmentation. Ces différents aspects du système de notation, alliés à des critères de conformité supplémentaires (e.g. non-concentration, volumétries minimales, conservatisme), appellent à des mécanismes de contrôle opérant à différents niveaux.
La définition statistique de l’homogénéité renvoie à l’application bijective associant un niveau de risque à un profil de risque. Autrement dit, il s’agit de s’assurer qu’un même paramètre de risque soit attribué à des populations de risques similaires. Le contrôle de cette association repose généralement sur une mesure quantitative et objective issue des méthodes d’inférence statistique.
Au-delà de ces statistiques, le contrôle de l’homogénéité passe par celui du processus de production des estimateurs des paramètres bâlois, en particulier sa robustesse à un environnement économique et juridique dynamique. Il convient donc de contrôler que les modèles soient bien appliqués à des populations cohérentes avec l’historique sur lequel ils ont été développés, ou que les grilles de scores restent fiables et exhaustives après leur implémentation dans les SI. Ceci dans le but de détecter l’émergence ou la disparition de facteurs de risque, ou une altération de leur régime d’association. Il est également nécessaire d’adresser la complexité du dispositif de notation, c’est-à-dire le nombre nécessaire (et suffisant) de modèles et de segments de calibrage. Ces notions renvoient directement à la variété des typologies de contrat et la granularité de la segmentation du portefeuille, qui ne se résument pas à une affaire de test statistique dès lors que l’on considère des critères supplémentaires, tels que les contraintes de volumétrie ou de matérialité opérationnelle. Nous reviendrons plus tard sur les contradictions pouvant apparaitre entre ces notions et celle de la significativité statistique. Aussi, conscients de la difficulté de satisfaire l’ensemble des critères de conformité des classes de risque, il convient de hiérarchiser ces critères afin de définir une méthodologie de contrôle lisible et applicable opérationnellement.
Enfin, les institutions bancaires mettent en place un système de gouvernance des modèles bâlois, établissant les rôles et responsabilités des différents acteurs et méthodes de contrôle. Il incombe à ceux-ci la définition de la stratégie 12 de notation, l’importance des contraintes opérationnelles, la philosophie de notation, ou encore le degré de liberté méthodologique des équipes de modélisation.
Pour autant, les aspects méthodologiques sont souvent intriqués dans ceux relevant de la gouvernance des modèles. Prenons à titre d’exemple le contrôle de la cohérence entre historique de modélisation et périmètre d’application, ou plus généralement la performance prédictive des modèles. Au-delà des aspects méthodologiques développés précédemment, il demande des campagnes de suivis des modèles, par ailleurs exigés par la réglementation. La mise en place de tels dispositifs, leur récurrence, leur caractère coercitif, et leur indépendance sont bien des éléments relevant de la gouvernance d’un dispositif bâlois.
Les mécanismes de contrôle
Ce qui est formalisé par la réglementation
A ce jour, si l’EBA introduit explicitement l’homogénéité des classes de risque comme un critère incontournable du dispositif bâlois, elle n’impose aucune définition formelle de l’homogénéité, ni aucune méthodologie de contrôle. Par ailleurs, les instructions de validation des modèles internes publiées par la BCE 13, définissant les exigences réglementaires en matière de backtesting des modèles IRB, ne proposent pas de test statistique d’homogénéité. Nous renvoyons le lecteur intéressé vers notre publication sur le backtesting réglementaire 14 pour plus de détails.
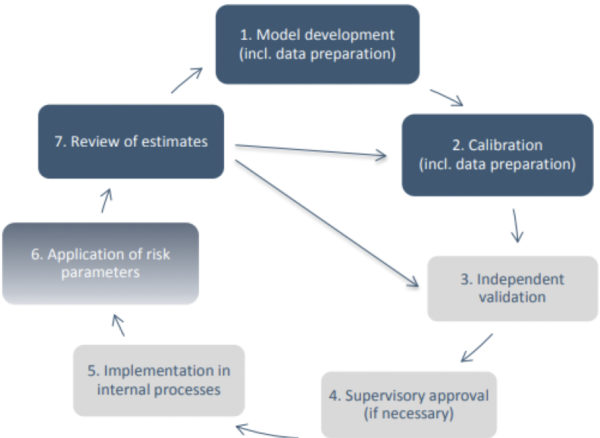
Les exigences en matière de gouvernance des modèles sont cependant clairement exposées dans les GL de l’EBA, notamment en ce qui concerne la revue régulière de la pertinence des estimateurs produits par les institutions, comme illustré ci-dessous par le cycle de vie du modèle Bâlois.
La littérature scientifique
Au meilleur de nos connaissances, il s’agit d’un sujet peu, voire non abordé dans la littérature scientifique. Même si les tests d’égalité des moyennes ou de distributions sont connus depuis longtemps, nous n’avons pas connaissance de recherches spécifiques liées à leur application dans le cadre du contrôle de l’homogénéité des classes de risque d’un modèle interne. Enfin, si les institutions bancaires portent une grande attention au sujet, elles se montrent encore réticentes à partager leurs travaux et leurs données avec les autres acteurs du secteur.
Les pratiques de place
Les observations issues de notre propre expérience, ainsi que les échanges que nous avons pu mener avec les professionnels du secteur, nous permettent d’esquisser les principales pratiques de place en matière de contrôle de l’homogénéité.
Les institutions bancaires distinguent visions univariées et bivariées. La première est centrée sur la question de la segmentation de la fonction de score 15 en classes de risques, et fait généralement l’objet de représentations graphiques fondées sur la variance intra classe du critère de risque (e.g. boite à moustache, intervalle de confiance), ou de tests de variance ou de permutation. La seconde considère le pouvoir de discrimination marginal d’un facteur de risque sur la classe ou la fonction de score. Nous retrouvons les tests usuels sur la tendance centrale (e.g. Student, Welch, Kruskall-Wallis) et des tests de distribution (e.g. EDF, Cramer Van Mises). L’interprétation de ces tests s’accompagne de contraintes de matérialité ou de stabilité, définies au regard de considérations opérationnelles propres à chaque portefeuille.
Nous pouvons noter une tendance à l’uniformisation des pratiques au sein des institutions liée au déploiement de standards de modélisation élaborés à l’échelle des groupes et appliqués au niveau des filiales. Cette tendance est également observable entre les institutions, du fait d’une grande mobilité professionnelle et un recours accru aux cabinets de conseil spécialisés, favorisant la diffusion des pratiques. Les esprits critiques noteront qu’à défaut de l’homogénéité des classes, nous observons une homogénéité des pratiques.
Toujours au regard de notre expérience, nous pouvons témoigner d’un recours fréquent du superviseur à l’approche bivariée, en particulier au test d’égalité des moyennes entre sous-populations d’une même classe de risque. Ces sous-populations étant le plus souvent identifiées par des variables binaires, qui ont pu être considérées lors du développement du score. L’approche univariée est généralement adressée au travers des questions de concentration des classes et du nombre de celles-ci.
Discussion
Les pratiques de place permettent-elles de répondre aux objectifs de contrôle de l’homogénéité ?
Une expérience des institutions relative aux missions d’audit qui révèle un contrôle du superviseur essentiellement statistique
Les approches méthodologiques développées par les institutions bancaires, ainsi que les mécanismes de gouvernance des dispositifs de notation bâloise qu’elles mettent en place, sont étroitement audités par le superviseur.
Ces contrôles sont le plus souvent motivés par une expertise métier et une expérience des pratiques de place. Puis, ces aprioris sont confirmés (ou infirmés) par un diagnostic technique, généralement un test statistique. Une fois la défaillance soulevée par le superviseur, la charge de la preuve de la matérialité renvient aux institutions supervisées.
Sans remettre en cause la rationalité de cette approche, il nous semble que ce diagnostic technique, essentiellement statistique, occulte les aspects méthodologiques développés plus haut. Une conséquence directe est l’omission de facto d’une problématique que l’on pourrait intituler « la recherche des critères contradictoires ».
L’échec des plans de correction ou la recherche de critères contradictoires
Rappelons-nous de la figure illustrant l’équilibre en les homogénéités inter et intra classe. Le score est la variable de discrimination du risque par excellence. Segmenter une classe de risque en fonction du score revient à discriminer les contreparties les plus risquées des moins risquées. Un test d’égalité des moyennes entre deux sous-populations discriminées par le score conclut, par construction, au rejet de l’hypothèse d’homogénéité de la classe testée. En l’absence d’autres critères, il est possible en principe de poursuivre ce mécanisme de segmentation à l’envie. Cette remarque vaut pour toute variable corrélée avec le score. Afin d’aider au diagnostic de l’information pertinente échappant au score, nous proposons dans l’encadré 2 un indicateur statistique mesurant le pouvoir discriminant marginal porté par une variable exogène.
L’adoption de l’approche bivariée ne va pas sans difficultés. Prenons le cas d’un test concluant au manque d’homogénéité d’une classe au regard d’une variable exclue du score pour cause de non-significativité. Nous observons alors une contradiction entre les critères de discrimination retenus lors du développement du score et ceux appliqués lors des tests d’homogénéité. Si les premiers mettent en avant des effets globaux et linéaires, les seconds portent sur des effets locaux (i.e. sur un segment du score) et potentiellement non-linéaires. Autant dire que cette configuration est à la fois fréquente, mais aussi insoluble. Par ailleurs, un plan de remédiation fréquent consiste en la segmentation de la classe par la variable testée. Nous observons alors le paradoxe d’attribuer plus d’importance à cette variable qu’à celles retenues dans le score. Nous passerons le problème de circularité, qui voit une classe segmentée perdre en discrimination (voire en monotonie) avec les classes adjacentes sur l’échelle de notation, appelant alors à des regroupements.
Considérons un score segmenté en classes. Le niveau de risque rk d’une classe est calculé comme la moyenne pondérée des niveaux de risque des notes de score associée à cette classe, notés rs . Pour toute classe k, l’écart de risque entre deux populations identifiées par un axe de discrimination 16 est calculé comme suit :
En cas de corrélation entre l’axe et le score, nous observons un écart de distribution des notes, la population la plus risquée regroupant davantage de notes faibles. Nous pouvons isoler l’effet de la distribution des notes en figeant les niveaux de risque rs,i de chaque note, les remplaçant par le niveau de risque de la classe rk,i .
De façon similaire, nous pouvons isoler l’effet de discrimination de l’axe en figeant la distribution des notes ns,i par population, remplacées par la distribution des notes de toute la classe nk,i .
La quantité GapDisc est donc une mesure de la part du pouvoir discriminant d’une variable exogène qui est orthogonal au score. Ainsi, l’écart de risque entre les deux populations vérifie la relation suivante :
Encadré 2 : Mesure marginal du pouvoir discriminant d’une variable exogène
Illustrons une autre problématique caractéristique des portefeuilles de type Retail, où il est fréquent d’observer un écart de risque moyen statistiquement significatif, bien que peu matériel d’un point de vue opérationnel. A distance finie, la distribution de la statistique de test sous l’hypothèse nulle (et donc la zone d’acceptation du test) couvre généralement un intervalle d’ordre de grandeur comparable avec celui de la matérialité opérationnelle. Considérons deux sous-populations présentant des taux de défaut moyen respectivement de 4,6 % et 4,7 %. Nous admettons volontiers que 4,6 % est différent de 4,7 %, mais nous ne sommes pas forcément sûrs de la précision de ces deux mesures pour rejeter l’hypothèse d’homogénéité. En revanche, lorsque de très grandes volumétries sont engagées (e.g. plusieurs centaines de milliers d’observations), la statistique de test sous H0 admet systématiquement une distribution resserrée. Nous considérons toujours 4,6 % différent de 4,7 %, mais nous sommes cette fois sûrs de la précision de chaque mesure, quand bien même l’écart mesuré ne serait pas matériel d’un point de vue opérationnel.
Ces exemples parleront à tout analyste ayant traité un jour du sujet. Ils illustrent l’illusion que représente la recherche de l’homogénéité des classes en restreignant la question à un problème purement statistique, peu importe in fine les tests retenus.
La nécessité de clarifier et hiérarchiser les critères de conformité des modèles
Il apparait alors nécessaire de prendre du recul sur les outils statistiques dans l’objectif de définir une méthodologie de contrôle de l’homogénéité des classes de notation. En effet, pour qu’une règle soit comprise et acceptée, il faut qu’elle soit claire dans son énoncé, et circonstanciée dans son contrôle. Nous pensons que la notion d’homogénéité n’est pas suffisamment exposée dans les textes réglementaires, amenant des divergences d’interprétation, et souvent réduite à sa seule dimension statistique. De plus, les pratiques de place en matière de contrôles nous paraissent restrictives, sans considération des aspects méthodologiques et des éléments de gouvernances qui assurent pourtant le contrôle régulier du portefeuille et des processus de production des estimateurs.
Par ailleurs, la considération de ces aspects méthodologiques serait pour le superviseur et les institutions bancaires l’occasion d’affirmer des principes communs de modélisation. Ceci en assumant une hiérarchie claire entre différents critères de conformités opérant à différentes étapes du processus de modélisation. Satisfaire à la saturation de l’information disponible, l’interprétabilité des modèles, tant leur performance que leur robustesse, une classification fine des contreparties sans trop d’échelons, etc., s’apparente souvent à la quadrature du cercle.
La vie du portefeuille et du modèle
De plus, il conviendrait de préciser la portée de ces contrôles en fonction de la position du modèle dans son cycle de vie. La question de l’homogénéité ne se pose pas en mêmes termes pour un modèle ancien ou un autre en cours de développement. Dans le premier cas, le contrôle de l’apport marginal d’un facteur de risque, à l’occasion d’un suivi par exemple, est primordial. Comme nous l’avons vu, il convient d’étudier la déformation du portefeuille depuis le développement du modèle afin d’évaluer le besoin de recalibrage, voire de refonte, si certains facteurs de risque émergent ou disparaissent.
La question de cette déformation ne se pose pas pour un modèle en cours de développement. Aussi, introduire les variables exclues de la modélisation dans processus de contrôle de l’homogénéité bivarié revient in fine à remettre en cause, même partiellement, les critères de sélection des facteurs de risque pertinents. Une même approche appliquée à différents moments peut mener à des incohérences.
Quelles pistes d’investigation peuvent être explorées ?
Une marge de manœuvre limitée pour les institutions bancaires
Nous proposons un bilan des réponses apportées par les institutions au défi que constitue l’homogénéité des classes et des marges de manœuvre dont elles disposent pour le surmonter. De façon générale, les institutions n’ont pas trouvé la « recette » de l’homogénéité, c’est-à-dire une méthodologie de modélisation et de contrôle qui réponde pleinement aux exigences réglementaires. Elles doivent souvent se livrer à des études complémentaires évaluant la matérialité de l’impact de l’hétérogénéité sur le montant de RWA. Celles-ci concluent généralement à la nécessité de mettre en place des marges de conservatisme, voire des add-ons aux fonds propres. En définitive, l’adoption d’une vision purement statistique offre peu de marges de manœuvre aux institutions bancaires.
Des exigences claires du régulateur, mais une mise en pratique loin d’être évidente
Ce tâtonnement méthodologique peut être rattaché au peu de certitudes qu’offre le cadre réglementaire. En effet, le flou entourant la définition de l’homogénéité appelle une grande marge d’interprétation des institutions bancaires, mais aussi du superviseur. Cela dit, les missions d’audit menées par ce dernier offrent l’opportunité d’un retour d’expérience qui permettront aux institutions de gagner en maitrise sur le sujet, et au superviseur d’expliciter ses attentes en la matière. Soit les deux ingrédients d’une harmonisation du cadre méthodologique.
Compléter la notion de statistiques par celles de méthodologie et de gouvernance
En parallèle, nous appelons à une complétude de la vision statistique par une dimension méthodologique, voire de gouvernance, pour adresser l’homogénéité à l’échelle du dispositif bâlois. Cela passe par une (re)définition de la place du critère d’homogénéité dans la réglementation bâloise. Par exemple, en complétant les tests statistiques par une évaluation qualitative des dispositifs mis en place par les institutions pour s’assurer de la performance des modèles au cours du temps, ainsi qu’une une redéfinition des exigences réglementaires en matière de publication. En particulier, nous plaidons pour une meilleure considération des indicateurs de stabilité du portefeuille. Nous avons vu que la notion d’homogénéité est liée à celle de la classification des contreparties ou contrats aux différentes classes de risque. Aussi, une évolution des interactions entre les variables exogènes et endogène est de nature à dégrader la performance des scores, et donc à favoriser un manque de conservatisme des paramètres calibrés. Enfin, nous plaidons pour une plus grande place réservée aux critères de matérialité, ainsi qu’une évaluation rationnelle du niveau de complexité induit par une recherche exhaustive d’homogénéité. Ces derniers aspects nous préservant d’un modèle victime de sur-apprentissage.
Quels apports des méthodes de Machine Learning ?
Nous avons discuté des critères de sélection des facteurs explicatifs du risque. En allant plus loin, nous pouvons légitimement nous demander si la question de l’homogénéité des classes n’est pas simplement une problématique de performance des modèles. Nous n’aborderons pas ici la question de la qualité et de l’exhaustivité des données, qui sont propres à chaque institution, mais poserons la question de savoir si les méthodologies standards de modélisation (e.g. régression linéaire, régression logistique, modèles experts) produisent des modèles capables de répondre aux exigences réglementaires.
La BCE conduit actuellement des consultations et des travaux portant sur l’application des méthodes d’apprentissage automatique 17. Cette famille de modèle 18 appartenant au domaine du Machine Learning (ML) revendique une capacité prédictive supérieure aux modèles classiques, basée sur leur capacité à trouver des structures d’association non-linéaires complexes, l’absence d’hypothèse de distribution, ainsi qu’une heuristique liée à la recherche du niveau de paramétrisation optimal. Cependant, quid de leur utilisation dans un cadre réglementaire exigeant un suivi étroit et une insertion opérationnelle dans les politiques courantes de la gestion du risque ?
Hurlin et Pérignon (2023) 19 proposent dans un excellent article une réflexion sur les enjeux de l’utilisation des méthodes de ML. S’il est vrai que l’utilisation de ces méthodes est répandue pour les phases exploratoires telles que la préparation des données ou la construction de modèles challengers, elle reste très limitée en ce qui concerne le développement du modèle de classification. En effet, l’un des principaux freins à l’utilisation de ces méthodes tient à la difficulté d’interpréter la plupart des modèles qui en résultent, même si plusieurs techniques ont été développées à cet effet : graphiques de dépendances partielles (Friedman, 2001) 20 ; graphiques des effets locaux cumulés (Apley et Zhu, 2020) 21 ; Local interpretable model-agnostic explanations (Ribero et al, 2016) 22 ; Shapley additive explanation (Lundberg et Lee, 2017) 23. D’autres méthodes, en revanche, permettent le développement de modèles nativement interprétables. Citons par exemple les algorithmes génétiques popularisés par Goldberg (1989) 24, ainsi que les méthodes PLTR (Dumitrescu et al, 2022) 25, et GAM(L)A (Flachaire et al, 2022) 26. Pour une revue complète de ces méthodes, nous renvoyons le lecteur intéressé vers l’article de Hurlin et Pérignon.
Pour ces approches, le coût de la performance se mesure au nombre de paramètres et d’hyperparamètres décrivant leur complexité, bien supérieure à celle des modèles classiques. Nous pouvons alors nous demander si les institutions bancaires sont prêtes à assumer ce coût, ou même si celui-ci est justifié. S’il ne nous appartient pas de répondre à ces interrogations, nous pouvons questionner la performance des approches de ML lorsqu’ils sont contraints au même nombre de paramètres que les modèles classiques.
Quoi qu’il en soit, le ML représente une réelle opportunité, tout en soulevant le besoin de définir une heuristique nouvelle, non pas fondée sur une notion de classification 27 ou de distance, mais sur celle d’homogénéité. En supposant une formalisation mathématique explicite, cette dernière pourrait conditionner des critères de performance ou d’arrêt permettant d’identifier les solutions les plus satisfaisantes sur le plan statistique comme opérationnel. Des approches simples, telles que les méthodes de partitionnement hiérarchique 28 peuvent se révéler particulièrement adaptées. Nous savons que l’adoption de ce type de méthode n’est pas anodine en matière de gouvernance aussi bien du côté des institutions bancaires que de celui du superviseur. Aussi, leur facilité d’interprétation, de suivi, et d’implémentation, allié à la souplesse de leur paramétrage en font des sujets d’étude pertinents. Peut-être une première étape avant une solution permettant une synthèse des exigences réglementaires et opérationnelles ?
Conclusion
L’objectif de cette publication est de questionner la place de l’homogénéité des échelons de notation dans un dispositif bâlois, ainsi que les modalités de contrôle de celle-ci. Après une brève introduction au formalisme bâlois, nous avons montré que l’approche ASFR ne saurait contribuer à une mesure prudente du risque de crédit en l’absence d’homogénéité des classes de risque sur lesquelles les paramètres bâlois sont appliqués. Nous avons exploré différentes causes d’hétérogénéité caractérisant un portefeuille de crédit. Ainsi, nous nous sommes intéressés à la variété des typologies de contrat, la dynamique de cette variété, ainsi qu’à la finesse avec laquelle celle-ci est appréhendée, soit la granularité de la segmentation du portefeuille. Une fois les causes identifiées, nous en avons explicité les conséquences d’un point de vue prudentiel, tant au niveau du segment de calibrage que du portefeuille lui-même. En particulier, nous avons mis en évidence le risque d’introduire un biais dans la mesure du risque de long-terme.
Une seconde partie est dédiée aux dispositifs de contrôle et de compensation observés dans l’industrie. En particulier, nous avons vu comment des marges de conservatisme pouvaient être calibrées afin de palier un défaut d’homogénéité, ou comment la définition de plusieurs segments de calibrages, voire plusieurs fonctions de score pouvaient adresser l’hétérogénéité du portefeuille. Puis nous avons introduit les trois niveaux de contrôle nécessaires à l’évaluation de l’homogénéité des classes : statistique, méthodologique et de gouvernance. Le premier, plus intuitif, renvoie au contrôle des niveaux de risques observés au sein du portefeuille, le plus souvent à l’aide de méthodes inférentielles. Cependant, la multiplicité des critères de conformité requiert une méthodologie de contrôle explicite assurant la hiérarchie d’indicateurs statistiques parfois contradictoires. Enfin, la place et la récurrence de ces contrôles renvoient à la gouvernance des modèles, tout comme le degré de contrainte que ces contrôles font peser sur le dispositif. Nous avons pu témoigner que les différentes parties prenantes n’accordaient pas la même attention à ces trois niveaux. En effet, seules les exigences en matière de gouvernance de modèle sont clairement posées par le régulateur, alors que les institutions bancaires se concentrent principalement sur le niveau statistique.
Dans la dernière partie de notre article, nous proposons une critique de l’efficacité des pratiques actuelles quant au contrôle de l’homogénéité. Nous avons dressé un constat d’échec de ces pratiques, en posant le diagnostic d’une recherche de critères souvent contradictoires. Aussi, nous avons montré la nécessité de considérer la vie du portefeuille et du modèle dans le choix et l’importance des indicateurs statistiques. Par ailleurs, nous avons proposé plusieurs pistes d’investigation pouvant être explorées, en soulignant le manque de marges de manœuvres à disposition des institutions bancaires, piégées dans une approche purement statistique du superviseur et un positionnement flou du régulateur. En particulier, nous proposons de compléter cette vision par une dimension méthodologique, en redéfinissant clairement la place de l’homogénéité dans la réglementation bâloise. Ceci en complétant les indicateurs quantitatifs par des évaluations qualitatives des mécanismes de contrôle auxiliaires tels que le backtesting, ainsi que par l’introduction d’indicateurs de stabilité, de matérialité et de complexité opérationnelle.
Nous avons enfin ouvert la discussion sur l’apport des méthodes de Machine Learning, en posant la question de l’homogénéité comme celle de la performance prédictive des scores. A date, ces méthodes sont loin de représenter la solution idoine, et le développement d’une heuristique nouvelle fondée sur le concept d’homogénéité nous semble nécessaire. Leur paramétrage complexe propose de nombreux défis en matière de gouvernance et de supervision. Cette problématique, à l’instar du risque climatique, constituera l’un des grands chantiers des acteurs du risque de crédit.
Bibliographie
- Genest B., Brie L. (2013) Basel II IRB Risk Weight Functions. Global Research & Analytics. 20/02/2013
- Basel Committee on Banking Supervision (2005) An Explanatory Note on the Basel II IRB Risk Weight Functions. July 2005
- Merton R. C. (1974) On the princing of corporate debt: The risk structure of interest rates. Journal of Finance 29, 449 – 470
- Vasicek O. (2002) Loan portfolio value. December 2002, 160 – 162
- Gordy M. B. (2003) A risk factor model foundation for rating based bank capital rules. Journal of financial intermediation, 2003
- European Banking Authority (2017) Guidelines on PD estimation, LGD estimation and the treatment of defaulted exposures. EBA/GL/2017/16.
- Regulation (EU) No 575/2013 of the European Parliament and of the Council of 26 June 2013 on prudential requirements for credit institutions and investment firms and amending Regulation (EU) No 648/2012
- EBA discussion paper on machine learning for IRB models. EBA/DP/2021/04
- Cadinot A. (2021) Backtesting règlementaire : Exercice complémentaire requis par la BCE. Atheïa Conseil, 2021
- ECB (2019) Instruction for reporting the validation results of internal models. February 2019
- Hurlin, Christophe and Pérignon, Christophe, Machine Learning and IRB Capital Requirements: Advantages, Risks, and Recommendations (June 19, 2023). Available at SSRN: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4483793
- Friedman (2001) Greedy function approximation: A gradient boosting machine. Annals of statistics, p. 1189-1232
- W. Apley, J. Zhu (2020) Visualizing the effects of predictor variables in black box supervised learning models. Journal of the Royal Statistical Society Series B: Statistical Methodology, 82(4):1059-1086
- Ribero, S. Singh, C. Guestrin (2016) “Why should I trust you?”: Explaining the predictions of any classifier. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, p. 97-101. June 2016
- Lundberg, S.-I. Lee (2017) A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems. NIPS’17, p. 4768-4777
- Dumitrescu, S. Hué, C. Hurlin, S. Tokpavi (2022) Machine leaning for credit scoring: Improving logistic regression with non-linear decision-tree effects. European Journal of Operational Research, 297(3): 1178-1192
- Flachaire, G. Hacheme, S. Hué, S. Laurent (2022) GAM(L)A : An econometric model for interpretable machine learning. arXiv
- Goldberg (1989) Genetic Algorithms in Seach, Optimization, and Machine Learning. Addison-Wesley Professional
- EBA/GL/2017/16 [↩]
- Merton R. C. (1974) On the pricing of corporate debt: The risk structure of interest rates. Journal of Finance 29, 449 – 470 [↩]
- Vasicek O. (2002) Loan portfolio value. Risk. December 2002, 160 – 162 [↩]
- Gordy M. B. (2003) A risk factor model foundation for rating based bank capital rules. Journal of financial intermediation, 2003 [↩]
- Ou contrats dans le cas d’un portefeuille de type Retail [↩]
- Regulation (EU) No 575/2013 of the European Parliament and of the Council of 26 June 2013 on prudential requirements for credit institutions and investment firms and amending Regulation (EU) No 648/2012 [↩]
- B. Genest, L. Brie (2013) Basel II IRB Risk Weight Functions. Global Research & Analytics. 20/02/2013 [↩]
- Certains portefeuilles peuvent nécessiter une segmentation apriori ou pré-segmentation [↩]
- Notons que dans le cadre d’un exercice de backtesting, la stabilité se mesure conjointement au pouvoir discriminant du modèle. [↩]
- Les défaillances introduisant un biais ponctuel seront adressées par la marge de catégorie C. [↩]
- Rappelons que l’influence de la LGD sur les RWA est linéaire, au contraire de celle de la PD, qui est concave. [↩]
- Nous faisons ici référence aux choix méthodologiques ou organisationnels structurant le système de notation. Nous n’employons pas le terme « philosophie de notation » afin d’éviter toute confusion avec le degré de sensibilité des modèles aux conditions macro-économique caractérisant les modèles Point-In-Time et Through-The-Cycle. [↩]
- ECB (2019) Instruction for reporting the validation results of internal models. February 2019 [↩]
- Cadinot A. (2021) Backtesting règlementaire : Exercice complémentaire requis par la BCE. Atheïa Conseil, 2021 [↩]
- Dans notre propos, une fonction de score désigne toute échelle ordinale du risque conditionnée par les caractéristiques des contreparties ou des contrats. Cette dénomination s’applique autant pour les modèles de PD que de LGD. [↩]
- Cet indicateur peut être généralisé à plus de deux populations, en appliquant des mesures de distances alternatives (ex : distance euclidienne multidimensionnelle). [↩]
- EBA/DP/2021/04 [↩]
- La qualification de modèle est discutable et le terme d’heuristique peut lui être préféré. En effet, ces approches visent à trouver des solutions acceptables (évaluées par une mesure de distance par rapport à une solution parfaite), sans se placer dans un cadre théorique formalisé. [↩]
- Hurlin, Christophe and Pérignon, Christophe, Machine Learning and IRB Capital Requirements: Advantages, Risks, and Recommendations (June 19, 2023). Available at SSRN: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4483793 [↩]
- J. Friedman (2001) Greedy function approximation: A gradient boosting machine. Annals of statistics, p. 1189-1232 [↩]
- D.W. Apley, J. Zhu (2020) Visualizing the effects of predictor variables in black box supervised learning models. Journal of the Royal Statistical Society Series B: Statistical Methodology, 82(4):1059-1086 [↩]
- M. Ribero, S. Singh, C. Guestrin (2016) “Why should I trust you?”: Explaining the predictions of any classifier. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations, p. 97-101. June 2016 [↩]
- M. Lundberg, S.-I. Lee (2017) A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems. NIPS’17, p. 4768-4777 [↩]
- D. Goldberg (1989) Genetic Algorithms in Seach, Optimization, and Machine Learning. Addison-Wesley Professional [↩]
- E. Dumitrescu, S. Hué, C. Hurlin, S. Tokpavi (2022) Machine leaning for credit scoring: Improving logistic regression with non-linear decision-tree effects. European Journal of Operational Research, 297(3): 1178-1192 [↩]
- E. Flachaire, G. Hacheme, S. Hué, S. Laurent (2022) GAM(L)A : An econometric model for interpretable machine learning. arXiv [↩]
- Le critère d’entropie adresse davantage la notion d’incertitude que celle d’homogénéité. [↩]
- Dont font partie les arbres de régression et classification. [↩]




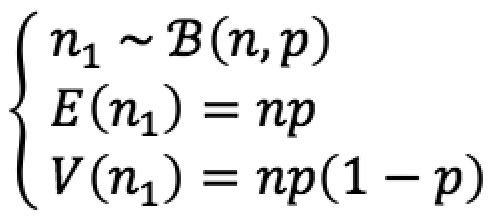
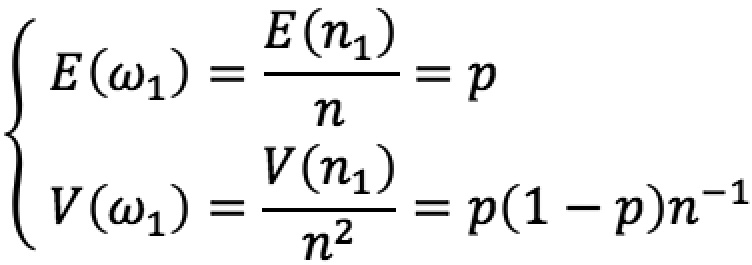
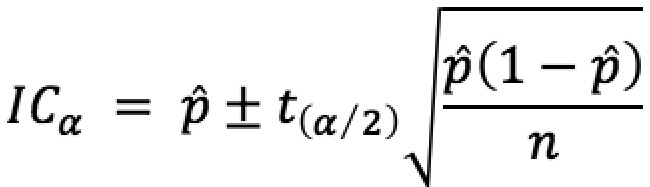
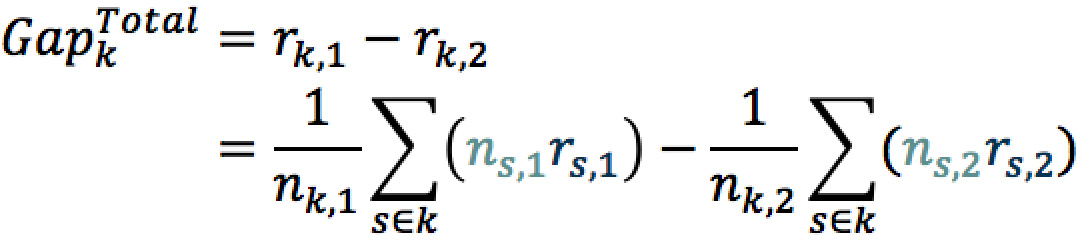
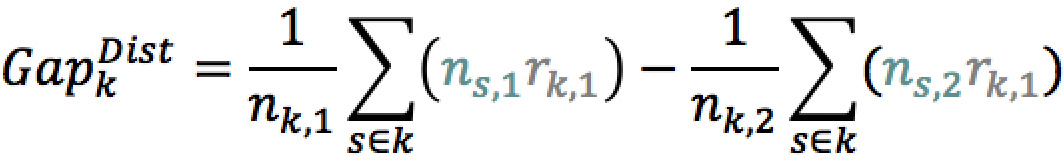
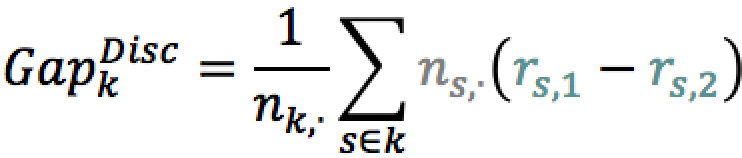
Sorry, the comment form is closed at this time.