Backtesting règlementaire Exercice complémentaire requis par la BCE
Application à un modèle de probabilité de défaut
Janvier 2021
Auteure
Alexandra Cadinot
Superviseurs
Eric Bataille
Olivier Gassner
Mise en contexte
Les institutions financières ont pour obligation d’effectuer au moins annuellement des exercices de backtesting, i.e. de contrôler la performance de leurs modèles internes utilisés dans l’approche IRB pour le risque de crédit.
Dans le cadre du mécanisme de supervision unique, la Banque Centrale Européenne (BCE) requiert désormais, et ce à partir du 31 décembre 2020, un exercice complémentaire dont elle a défini les modalités et les tests. Un dossier annuel sera désormais envoyé à la BCE pour chaque modèle, comprenant : le rapport de backtesting interne, le rapport de validation interne correspondant, ainsi que les résultats des mesures et tests prescrits, sous la forme d’un fichier Excel préformaté par le Régulateur.
Cet article a pour objectif de vous aider à comprendre le fonctionnement et la sensibilité des tests demandés par la BCE, ainsi que leur complémentarité avec les tests généralement retenus pour la validation interne et ce, à travers l’exemple d’un modèle de probabilité de défaut.
Pour ce faire, le document s’articule autour des trois composantes d’analyse couramment retenues pour un backtesting : la stabilité de la population, le conservatisme de l’estimateur et enfin le pouvoir discriminant du modèle. Chacun des volets présente tout d’abord la ou les mesures demandées par la BCE, puis le lien avec les tests habituellement utilisés en interne, afin de mettre en évidence leur complémentarité.
Descriptif du modèle
Le modèle de notation utilisé a été développé sur un portefeuille hypothécaire américain pour une période allant de mars 2003 à novembre 2014 et sera soumis à un exercice de backtesting pour la période allant de décembre 2014 à décembre 2015. Il présente un volume actuel d’environ 700 contrats pour un encours de 85 M€, et un risque global de 3%. Ce modèle peut être qualifié d’hybride à prévalence Through-The-Cycle (TTC), construit à partir d’une dimension socio-démographique fondée sur le score à l’origine de l’emprunteur auquel viennent s’ajouter des facteurs macroéconomiques. Un modèle TTC est un modèle de notation qui est caractérisé par peu de migrations entre classes de risque, et des taux de défauts par classe fluctuants.
De façon générale, le modèle TTC n’est presque pas affecté par les conditions économiques, contrairement à un modèle Point-in-Time (PiT), qui, lui, suit le cycle économique et donc se caractérise, à l’inverse, par des migrations plus significatives entre les classes de risque, et des taux de défaut par classe relativement stables.
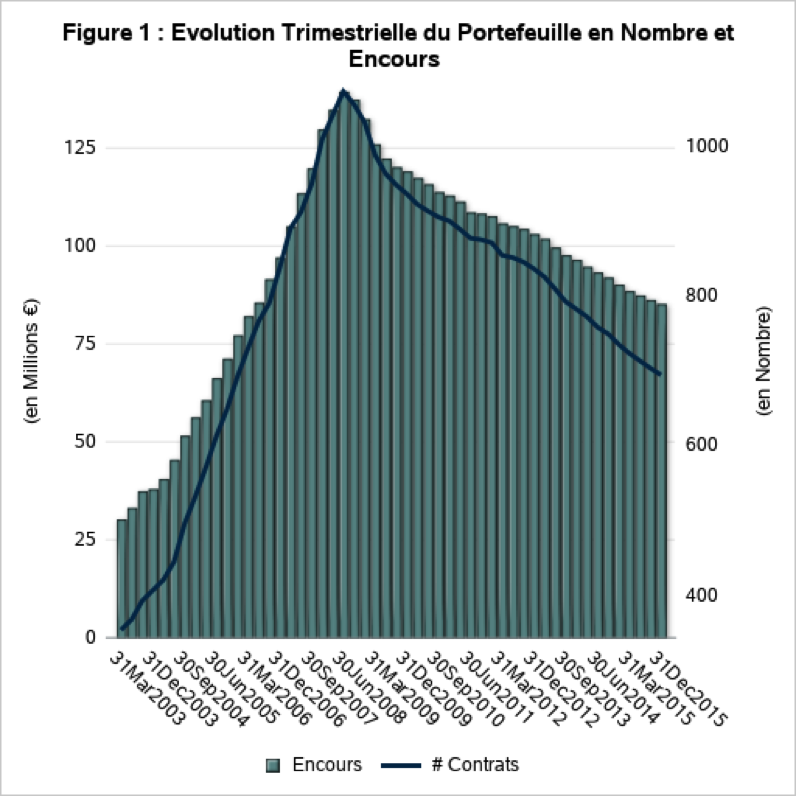
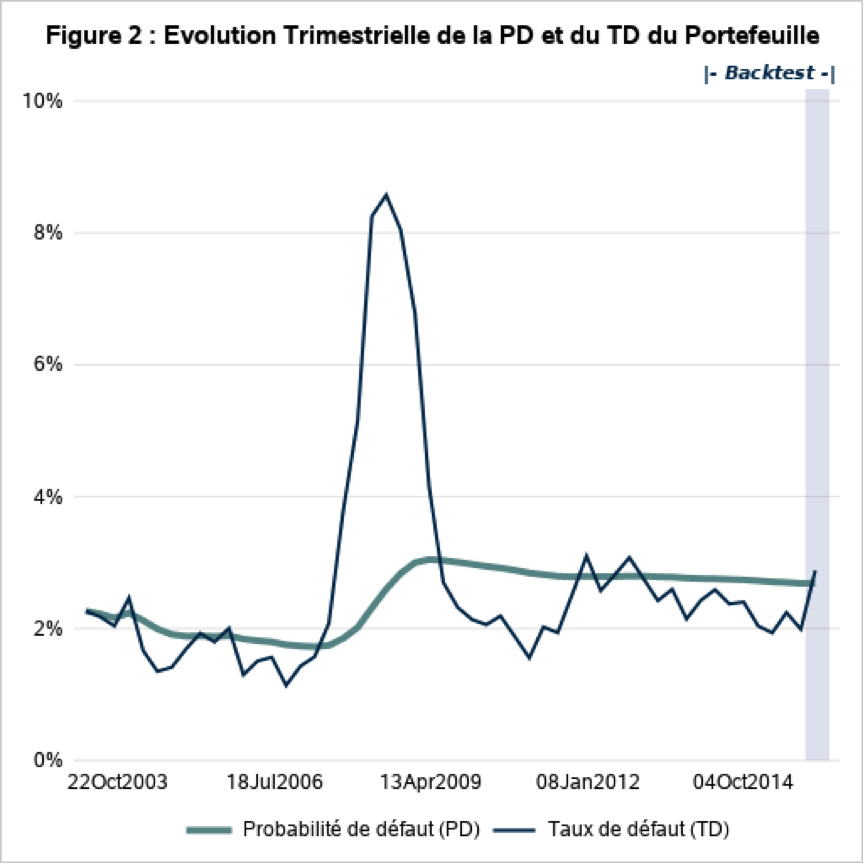
On observe clairement les effets de la crise financière de 2008 sur les Figures 1 et 2. En effet, sur la période antérieure à la crise, le portefeuille se trouve dans une phase de développement très rapide, l’exposition globale du portefeuille étant multipliée par 5 en 5 ans pour atteindre plus de 130 M€, et un nombre de contrats dépassant le millier. Tandis que sur la période postérieure à la crise, le portefeuille se situe plutôt sur une phase décroissante avec un nombre de contrats qui a diminué de près d’un tiers pour un montant total d’exposition de 85 M€, soit une baisse de près de 35 %. Le risque global du portefeuille a lui aussi été impacté par la crise, pour atteindre un taux défaut de près de 9 % avant de se stabiliser par la suite un niveau autour de 3 %.
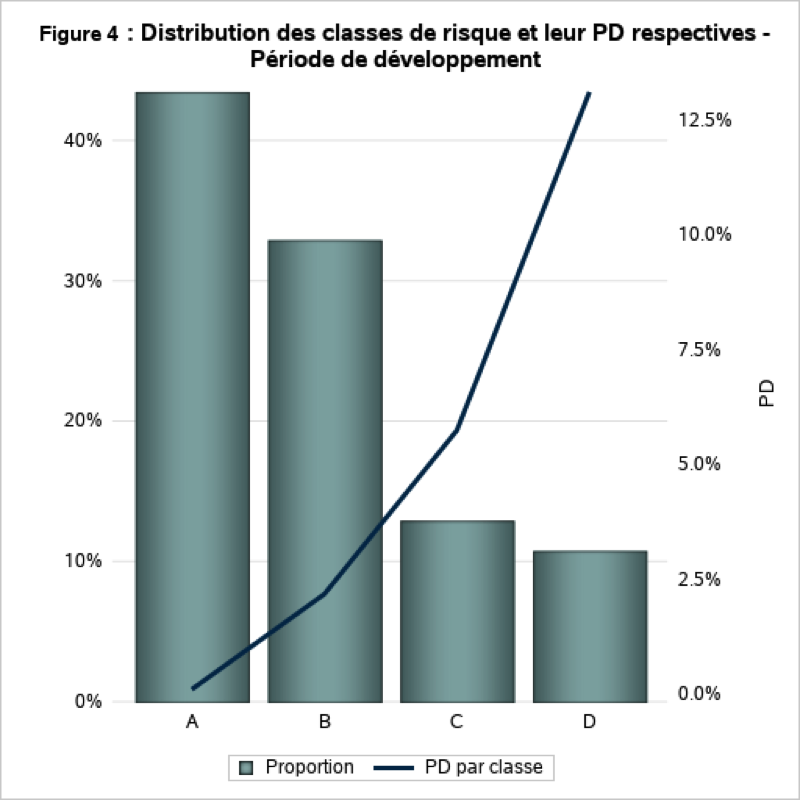
La Figure 4 nous montre la distribution des classes de risque ainsi que la probabilité de défaut associée pour la période de développement. On constate que le portefeuille est composé à plus de 75 % par les classes de risque A et B (les moins risquées) avec un risque associé respectivement de 0,9 % et 2,2 %.
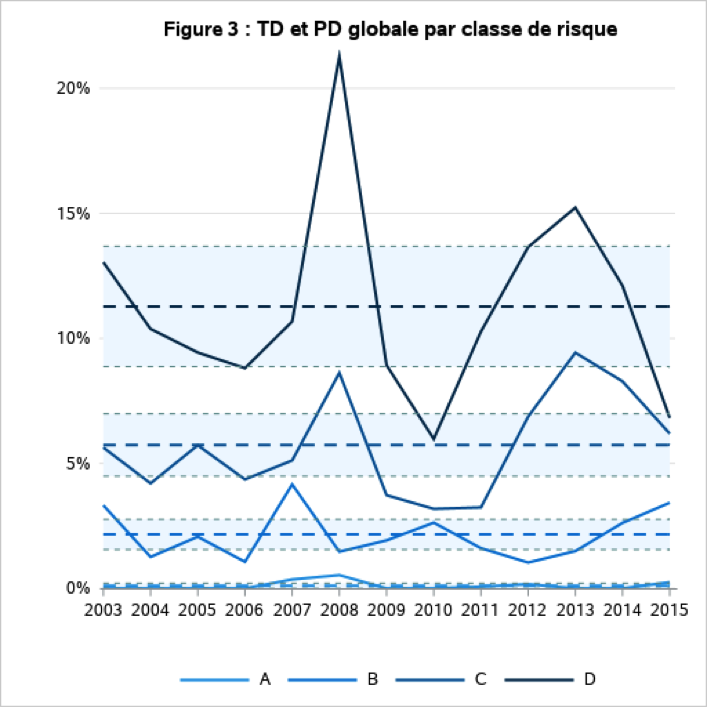
La Figure 3 nous montre l’évolution du taux de défaut ainsi que la probabilité de défaut par classe de risque sur l’ensemble de la période de développement. On constate que la crise de 2008 a eu un impact sur les taux de défaut sur l’ensemble des classes de risque avec un effet plus prononcé sur les plus risquées. Cet effet peut être expliqué par le fait que, le portefeuille est composé de produits hypothécaires américains et qu’une partie des contrats, qui constituent ces classes de risque, n’auraient probablement pas été octroyées aujourd’hui au vu de leur profil de risque.
La seconde hausse des taux de défaut observée entre 2011 et 2013 pour les classes de risque les plus risquées (C et D) s’explique en partie par leur faible volumétrie, les rendant ainsi très sensibles à de faibles changements du nombre de défauts.
Stabilité de la population
La première composante de l’exercice règlementaire permet d’évaluer la stabilité du modèle de notation sur la dernière année observée, ce qui dans notre cas, correspond à la période allant de décembre 2014 à décembre 2015. L’évaluation de cette stabilité se fait selon trois axes : les migrations des expositions, la stabilité de la matrice de migration, ainsi que la concentration des classes de risque.
1. Migrations des expositions (MWB)
Les deux premiers indicateurs “Matrix Weighted Bandwidth” (MWBU et MWBL) calculés à partir de la matrice de migration, représentent le pourcentage de migrations effectives à la hausse (resp. à la baisse) sur le nombre maximum de migrations possibles. Les mesures sont calculées au niveau portefeuille.
Le calcul de ces indicateurs se fait de la façon suivante 01
où ∶
- K est le nombre de classe de risque ;
- Ni est le nombre d’expositions dans la classe de risque i au début de la période d’observation ;
- pij est la fréquence relative des migrations entre les classes de risque i et je ;
- Nij est le nombre d’expositions se trouvant dans la classe de risque i au début de la période d’observation et dans la classe j à la fin de cette même période.
Notons que la BCE a fait le choix de ne pas accompagner ces indicateurs d’une grille de lecture. Les valeurs de ces derniers pouvant varier entre 0 et 1, nous pouvons tout de même déduire qu’une valeur proche de 0 est souhaitable pour montrer une stabilité des expositions. En effet, plus les valeurs seront proches de 0 et plus les migrations se situeront autour de la diagonale. A l’inverse, des valeurs proches de 1, impliquent de fortes migrations dans les classes de risque plus éloignées de la classe de risque à la période initiale (par exemple, migration de la classe A vers D, C vers A, etc.). Ce type de migrations est généralement caractéristique d’un portefeuille volatile ou d’un modèle de notation peu discriminant.
En effet, des migrations extrêmes révèlent un comportement imprévisible du portefeuille. Le modèle sous jacent présentera donc des difficultés à cerner le risque et dans ce cas, à discriminer les expositions ayant un risque élevé de celle avec un risque plus faible.
De plus, si la population lors du développement est différente de celle du backtesting, le calibrage réalisé lors du développement entrainera des précisions erronées sur la période de backtesting. Le risque supposé ne sera probablement pas représentatif du risque actuel du portefeuille.
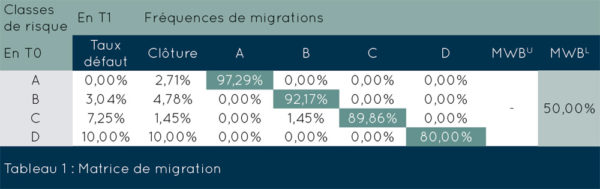
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
On constate que le MWBU est manquant, ce qui s’explique par le fait que nous n’avons aucune migration dans la partie supérieure de la matrice. Le MWBL quant à lui signifie que les migrations effectives représentent 50% des migrations maximales possibles. À première vue, la valeur peut sembler un peu élevée, mais les seules migrations observées sont adjacentes à la diagonales (classe C vers B), soit une migration d’une note sur les 2 possibles.
Ce résultat est donc tout à fait satisfaisant pour la stabilité de notre population. Dans notre cas, vu le faible nombre de migrations, il est pertinent de mettre en relation les fréquences de la matrice de transition avec les résultats des mesures MWBU et MWBL afin d’éviter de mauvaises interprétations.
Les deux indicateurs sont extrêmement sensibles aux migrations et ce, quelque soit le pourcentage de ces migrations. En effet, que ce soit une très forte ou une très faible partie de la population qui migre, l’indicateur donnera le même résultat. Par exemple, un MWB de 100% nous indiquerait que les migrations sont à l’extrême de la diagonale, or ce résultat peut également être obtenu si dans notre modèle nous avons une migration de la classe C vers la classe A d’une très faible partie de la population. Cela ne signifie pas pour autant que notre population a perdu de sa stabilité. Ainsi, une même valeur de MWB peut résulter de matrices de migrations très différentes. La mesure seule, malgré sa pertinence, ne suffit pas à son interprétation.
De plus, nous pensons qu’un MWB de 50% calculé sur un modèle de notation TTC avec une distribution des niveaux de risque stable dans le temps ne doit pas être interprété de la même façon que cette même valeur calculée sur un modèle PiT avec une population qui a tendance à migrer davantage. En effet, dans un cas, la mesure peut révéler un changement de population tandis que dans l’autre, cela s’apparente à un comportement normal reflétant la philosophie du modèle sous-jacent. La sensibilité du MWB aux facteurs externes fait, qu’une même valeur, pourrait aboutir à deux conclusions différentes.
Par conséquent, il nous semble pertinent de prendre en compte dans l’interprétation des valeurs de ces mesures d’autres paramètres, tels que la philosophie du modèle ainsi que les fréquences de migration en elles-mêmes.
La complémentarité des tests requis par la BCE avec les tests généralement retenus pour la validation interne décrit en introduction sera abordée par la suite.
2. Stabilité de la matrice de migrations Z-tests
La seconde métrique Zij s’assure de la monotonie des fréquences de migration en dehors de la diagonale au moyen de Z-tests, identifiant ainsi les changements possibles de population au sein du portefeuille. L’hypothèse nulle peut être décomposée en deux sous-tests disjoints, à savoir 02 :
- Partie supérieure de la matrice de migration : pour une classe de risque fixée, la fréquence de migration vers une classe de risque doit être inférieure à la fréquence de migration vers une classe de risque , où est plus risquée que . En d’autres termes, les fréquences de migrations pour une classe de risque donnée doivent être décroissantes pour cette partie de la matrice.
- Partie inférieure de la matrice de migration : pour une classe de risque fixée , la fréquence de migration vers une classe de risque doit être supérieure à la fréquence de migration vers une classe de risque où est plus risquée que . En d’autres termes, les fréquences de migrations pour une classe de risque donnée doivent être croissantes pour cette partie de la matrice.
Notons que la BCE a fait le choix de ne pas accompagner ces indicateurs d’une grille de lecture même si, pour ces mesures, l’usage des p-values restreint le champ des possibilités.
Nous avons opté pour la grille de lecture suivante :
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
Les p-values obtenues sont toutes supérieures à 10%, et ce, à cause du très faible nombre de migrations de la population constituant notre portefeuille. Par conséquent, nous ne disposons pas de suffisamment d’éléments pour rejeter l’hypothèse nulle.
Le résultat est tout de même satisfaisant puisque nous sommes en présence d’un modèle TTC avec une matrice de migration où les fréquences sont principalement concentrées sur la diagonale et la monotonie de ces dernières est clairement respectée (cf. le tableau 1 page 4).
La mesure de la monotonie des fréquences de migrations Zij, de par sa construction, pourrait générer des problèmes de sensibilité en cas de population à fortes volumétries. En effet, l’intervalle de confiance étant très précis, le moindre changement aussi faible soit-il, pourrait engendrer un rejet de l’hypothèse nulle. Par conséquent, une étude de sensibilité du test à la volumétrie pourrait être apportée par l’établissement pour les portefeuilles concernés, afin d’introduire une notion de tolérance dans les écarts, qui ne serait plus d’ordre statistique mais plutôt d’ordre opérationnel.
3. Concentration des classes de risque
Le dernier indicateur de stabilité permet d’évaluer si les classes de risque se dispersent de façon significative. En d’autres termes, cet indicateur nous permet de comparer le niveau de concentration actuel versus celui calculé sur la période de développement du modèle. Veuillez noter que, plus les classes de risque sont uniformément distribuées, plus la valeur du niveau de concentration à savoir, Herfindahl Index (HI) sera élevée.
Le calcul du coefficient de variation et du niveau de concentration se fait de la façon suivante :
où :
- K est le nombre de classes de risque pour les expositions en non défaut ;
- Ri est la fréquence relative de la classe de risque au début de la période d’observation.
La p-value ![]() est ensuite calculée, où représente la fonction de distribution cumulative de la loi normale et est le coefficient de variation calculé sur la période de développement 03.
est ensuite calculée, où représente la fonction de distribution cumulative de la loi normale et est le coefficient de variation calculé sur la période de développement 03.
Notons que la grille de lecture des p-value présentée précédemment, a été appliquée ici (cf. Tableau 2).
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
Le niveau de concentration actuel, pondéré en nombre de contrats, n’est pas significativement supérieur à celui du développement. En effet, d’après la Figure 3, la distribution des classes de risque ne présente pas de concentration sur une classe de risque spécifique. De plus, les niveaux de concentration actuels, pondérés en nombre de contrats ou en encours, sont relativement proches (38,67 % vs. 38,28 %).
Veuillez noter que, la p-value est calculée uniquement avec les niveaux de concentration pondérés en nombre car, la pondération en encours n’a pas été retenue par la BCE pour effectuer le test statistique.
Globalement, les différentes mesures nous montrent que la population constituant notre portefeuille est stable entre la période de validation et celle ayant servie au développement.
La mesure du niveau de concentration est, par construction, directement liée à la distribution des classes de risque. Elle sera donc plus sensible dans le cas d’un modèle de notation PiT puisque les migrations sont plus significatives pour ce type de modèle. Par conséquent, le rejet de l’hypothèse nulle sera donc plus fréquent que pour des modèles de notation TTC, et ce, quelle que soit la conjoncture économique.
De plus, le niveau de concentration est également sensible à la pondération qui lui est associée, i.e. un niveau de concentration pondéré en nombre pourrait être vraiment très différent du niveau de concentration pondéré en encours et ce, pour la même période. Cette problématique concerne surtout les portefeuilles ayant d’importants montants d’encours par exposition, notamment les Low Default Portfolios (Corporate, Souverains, etc.).
Prenons par exemple, un cas où un nouveau contrat avec une exposition suffisamment conséquente pourrait venir modifier la distribution en encours actuelle du portefeuille de façon significative. Cependant, cette modification n’étant introduite que par un seul nouveau contrat, la distribution en nombre de contrats peut, elle, rester stable par rapport à la période de développement.
Dans ce cas, l’hypothèse nulle ne serait pas rejetée, puisque la p-value est fondée sur le niveau de concentration pondéré en nombre de contrats, mais la valeur du niveau de concentration nous indiquera qu’il existe bien un changement dans le portefeuille dont il en sera tenu compte dans l’application actuelle du modèle.
4. Tests généraux retenus en interne
L’exercice de backtesting interne doit s’assurer de la stabilité de la population entre la période de développement et la période actuelle.
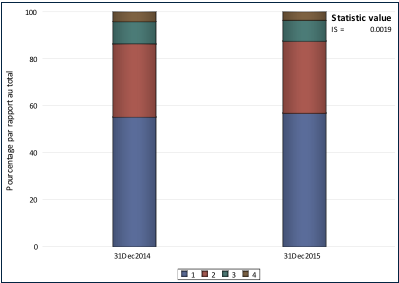
Généralement, une évolution graphique des classes de risque est fournie et accompagnée d’une valeur d’agrégation comme l’indice de stabilité de la population (IS). La représentation graphique permet de s’assurer visuellement qu’il n’y a pas une différence marquante entre la population actuelle et celle lors du développement. Elle permet également d’illustrer le résultat de la valeur d’agrégation accompagnant le graphique.
L’indice de stabilité permet de mesurer la différence des distributions de deux populations comme par exemple, la distribution actuelle du score et celle lors du développement. Veuillez noter que le découpage du score peut être fait en déciles ou en classes de risque.
Le calcul de la mesure se fait de la façon suivante :
où :
- K est le nombre de classes de risque pour les expositions en non défaut ;
- %Initk est la fréquence relative de la classe de risque K au début de la période de développement ;
- %Currk est la fréquence relative de la classe de risque K au début de la période d’observation actuelle.
On considère qu’il existe une différence de population pour une valeur de l’IS supérieure à 10%.
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
Comme le confirme les distributions des classes de risque et la valeur de l’IS, la population actuelle et celle utilisée pour le développement du modèle ne présente pas de différence significative.
Notons que l’indice de stabilité compare les distributions entre deux périodes sans tenir compte des migrations en tant que telles, i.e. l’IS nous montrera qu’il existe ou non une différence entre la distribution actuelle et celle de la période de développement, tandis que les mesures de la BCE viennent davantage nous renseigner sur la nature de cette différence de population.
Par conséquent, des divergences de conclusion entre les mesures usuelles et celles requises par le rapport complémentaire pourraient subvenir puisque les mesures ne s’intéressent pas aux mêmes aspects de la population. Cette problématique est susceptible d’apparaitre davantage dans le cas des modèles PiT, puisque ces derniers sont plus sujets à des migrations significatives de leur population.
Le Herfindahl Index (HI) pondéré en encours illustre également une autre dimension de la stabilité du portefeuille face au risque ne pouvant être reflété par les autres mesures de stabilité fondées sur le nombre de contrats. En effet, comme nous l’avons expliqué précédemment, l’introduction d’un contrat avec un montant d’exposition différent de ceux habituellement constaté, pourrait passer inaperçu avec des mesures de stabilité usuelles reposant sur le nombre de contrats. Or, il nous parait important d’en avoir connaissance et de le documenter, et ce même si cela ne remet pas en cause la performance du modèle sous revue.
Conservatisme de l’estimateur
1. Test de Jeffreys
Cette mesure permet d’évaluer le conservatisme de l’estimateur de Probabilité de Défaut au niveau du portefeuille ainsi que, de chaque classe de risque. En d’autres termes, ce test nous permet de nous assurer que le nombre de défauts observés n’excède pas statistiquement le nombre de défauts attendus correspondant à la Probabilité de Défaut (PD) calibrée sur l’échantillon de développement.
Le test de Jeffreys est construit en calculant la p-value ![]() est la fonction de distribution de la loi Beta avec les paramètres
est la fonction de distribution de la loi Beta avec les paramètres ![]() , et ce, au niveau du portefeuille global et pour chacune des classes de risque. Ici, est le nombre d’expositions du portefeuille ou de la classe de risque et est le nombre de ces expositions pour lesquelles un défaut est survenu durant la période d’observation. Comme souligné précédemment, le test est requis au niveau du portefeuille global et pour chacune des classes de risque 04).
, et ce, au niveau du portefeuille global et pour chacune des classes de risque. Ici, est le nombre d’expositions du portefeuille ou de la classe de risque et est le nombre de ces expositions pour lesquelles un défaut est survenu durant la période d’observation. Comme souligné précédemment, le test est requis au niveau du portefeuille global et pour chacune des classes de risque 04).
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
On constate qu’au niveau portefeuille, l’hypothèse H0 selon laquelle l’estimateur PD ex ante est supérieur à la PD ex post (observée), n’est pas rejetée. Cependant, de façon plus granulaire, cette hypothèse est rejetée uniquement pour la classe de risque A, en raison de la faible volumétrie des défauts, ce qui rend le test très sensible pour cette classe. En effet, pour la période considérée, on observe seulement deux défauts pour la classe de risque A, ce qui nous conforte sur le conservatisme de l’estimateur, et ce, malgré le rejet de l’hypothèse nulle.
De façon générale, au regard de la philosophie TTC du modèle de notation et de la nature du Test de Jeffreys, nous nous attendons à rejeter l’hypothèse nulle fréquemment puisque par définition, les fluctuations des taux de défaut du modèle TTC autour de la moyenne conduira à rejeter davantage l’hypothèse nulle que pour un modèle PiT.
On peut s’interroger sur la philosophie sous-jacente au test de Jeffreys. En effet, le test compare ici le paramètre qui est issu d’une moyenne long terme à un taux de défaut ponctuel. Dans le cadre d’un modèle PiT où les taux de défauts sont relativement stables au cours du temps, une comparaison avec un taux de défaut ponctuel semble plus intuitive que dans le cas d’un modèle TTC. De plus, la sensibilité du modèle PiT aux conditions économiques permet de produire des estimations ex ante proches des taux de défaut ex post au niveau du portefeuille.
Cependant, dans le cas d’un modèle TTC, les taux de défauts ponctuels peuvent varier fortement. Il nous semble qu’un test de comparaison entre deux moyennes de long terme serait mieux adapté. Le sujet sera davantage abordé à la section suivante. Cependant, le test de Jeffreys pourrait dans ce cas, être considéré non pas en tant que reflet de la capacité prédictive du modèle mais en tant que signal avancé d’un possible changement de tendance dans le portefeuille.
2. Tests généraux retenus en interne
L’exercice de backtesting interne doit s’assurer de la validité actuelle du paramètre de risque estimé sur la période de développement. En d’autres termes, l’exercice de backtesting permet de garantir que le nombre de défauts effectivement observé sur la période actuelle est statistiquement couvert par l’estimateur PD ex post.
Généralement, les tests utilisés lors d’un backtesting interne sont les suivants :
- au cas où le test disjoint est retenu, à savoir par classes de risque, le test binomial peut être réalisé. Il compare l’hypothèse nulle selon laquelle la PD estimée est égale au taux de défaut observé pour une classe de risque spécifique. Un pré requis au test est que le portefeuille soit homogène, que les évènements de défauts soient indépendants et suivent une distribution normale. Cette hypothèse est souvent respectée au vu de la taille des échantillons considérés. Un ajustement de type Bonferroni 05 peut être ajouté afin de proposer une conclusion unique à un ensemble de tests disjoints.
- au cas où le test joint est retenu, à savoir sur l’ensemble du portefeuille, le test Hosmer-Lemeshow peut être réalisé. La statistique d’Hosmer-Lemeshow suit une distribution du à k degrés de liberté, où k est le nombre de classes de risque. L’hypothèse nulle testée est que, l’ensemble des PD estimées pour chacune des classes de risque coïncide avec les taux de défauts observés. Un pré requis au test est l’indépendance et l’approximation normale des évènements de défauts. En d’autres termes, les évènements de défauts doivent converger vers une loi normale de manière asymptotique. L’hypothèse d’indépendance est très importante car dans le cas des portefeuilles à faible volumétrie, un faible changement dans la distribution des classes de risque pourra avoir un impact important sur la statistique d’Hosmer-Lemeshow.
- au cas où l’indépendance des évènements de défauts n’a pu être démontrée statistiquement, le test normal peut être réalisé de façon disjointe sur chacune des classes de risque. Le test est appliqué sous l’hypothèse que le taux de défaut moyen ne varie pas énormément à travers le temps et que les évènements de défauts survenus sur différentes années sont indépendants. Un ajustement de type Bonferroni peut également être ajouté afin de proposer une conclusion unique à un ensemble de tests disjoints.
Les résultats des tests d’Hosmer-Lemeshow obtenus à partir de notre modèle de probabilité de défaut sont repris et commentés plus bas (Tableau 6).
Les tests binomiaux ont été réalisés selon deux stratégies différentes (Tableau 5). Dans un premier temps, le paramètre PD qui est une moyenne de long terme, a été comparé avec le taux de défaut dit ponctuel, reposant sur les données de la dernière année. Nous observons des résultats similaires au test de Jeffreys. En effet, tous deux se concluent par un rejet de l’hypothèse H0 pour la classe de risque 1.
Dans un second temps, nous avons opté pour un test plus en adéquation avec la philosophie TTC de notre modèle. Le paramètre PD a donc été comparé cette fois-ci, à la moyenne de long terme ajustée avec les données de la dernière année. Dans ce cas, les résultats obtenus sont quelque peu différents.
En effet, le rejet de H0 est observé cette fois pour la classe de risque 4 qui est la plus risquée. Ce rejet peut être surprenant à première vue, puisse que le test compare une valeur de paramètre PD de 11,28% avec un TD ponctuel de 16,67% et respectivement une moyenne de long terme de 13,10%. Malgré le fait que la moyenne de long terme soit inférieure au TD ponctuel, ceci peut être expliqué par la volumétrie des observations de la classe 4 (24 observations pour le calcul du TD ponctuel contre 4 321 pour la moyenne de long terme). En effet, l’intervalle de confiance autour du TD ponctuel étant beaucoup plus large, l’hypothèse nulle n’est donc pas rejetée dans ce cas.
Le test d’Hosmer-Lemeshow, comme le montre le tableau ci-dessous, conclut à un rejet de H0 contrairement au test de Jeffreys au niveau global.
Ce résultat peut paraitre surprenant puisque les deux tests comparent les défauts observés sur la même période, à savoir la dernière année. Cependant, le test de Jeffreys étant un test de conservatisme, il vient s’assurer que l’estimateur PD ex ante couvre suffisamment les défauts observés ex post. Le test d’Hosmer-Lemeshow, quant à lui, est un test de précision, la PD ex post de chaque classe est comparée à son estimateur ex ante, afin de construire une statistique de, comme on comparerait une distribution observée a une distribution théorique sous H0. Par conséquent, il est tout à fait justifiable d’obtenir des conclusions différentes.
Le choix du test retenu par le backtesting interne dépend de la philosophie du modèle ainsi que la stratégie envisagée. En d’autres termes, l’exercice de backtesting interne peut choisir de tester la précision de l’estimateur et pas seulement le conservatisme. On pourra également vouloir distinguer la précision de la moyenne de long terme et la marge de conservatisme, notamment pour s’assurer de la validité du calibrage. Le but étant de voir si la moyenne de long terme correspond toujours au volume de défauts observés durant la dernière année sans tenir compte de la marge de conservatisme.
Un aspect tout aussi important du test utilisé lors de cet exercice est la probabilité est comparée. En effet, dans le cas d’un modèle TTC, l’établissement peut avoir opté pour le choix de comparer non pas le TD ponctuel de la période backtestée, mais la moyenne de long terme des taux de défaut sur la période globale à laquelle ont été ajoutées les observations de la dernière année. En effet, ce type de test peut sembler plus approprié dans le cadre d’un modèle TTC, dans la mesure où, les taux de défaut ponctuels y fluctuent davantage que ceux des modèles PiT. Dans ce cas, le test de Jeffreys, viendrait apporter une information complémentaire sur les taux de défauts ponctuels, contrairement au test interne qui, nous informe plutôt sur la moyenne de long terme des taux de défaut.
Pouvoir discriminant du modèle
1. Variation de l’AUC
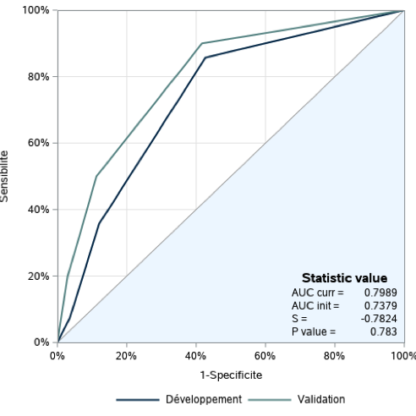
Cet indicateur nous permet à l’aide de l’AUC, d’évaluer si la capacité du modèle à discriminer correctement les expositions risquées des moins risquées a diminuée de façon significative.
Le calcul de la statistique se fait de la façon suivante 06 :
![]()
où représente l’AUCinit calculé sur la période de développement, représente l’AUCcurr sur la période d’observation actuelle et représente l’écart-type estimé de l’AUCcurr
Dans le cas des Low defaults Portfolio (LDP), une transformation préalable à la construction de la statistique est requise.
Encadré : Test AUC sur les Low Default Portfolio
La BCE fait mention dans ses guidelines (2) de l’importance de la profondeur des échantillons et du traitement appliqué aux données.
En effet, dans le cas des LDP, le nombre de défauts sur une année n’étant pas suffisant, la BCE requiert l’utilisation d’une période plus large, soit un historique de trois ans. Cependant, une transformation des classes de risque doit être faite afin de rendre l’AUC commensurable sur l’ensemble de la période.
La transformation consiste à réaffecter une nouvelle classe indépendamment de la classe de risque issue du modèle de notation. La nouvelle classe n’est autre que la fréquence cumulée de la distribution de la classe de risque à laquelle appartient l’exposition et ce, pour chacune des années de la période considérée.
Prenons par exemple, un modèle de notation sur un LDP avec deux classes de risque A et B, A étant la classe la moins risquée.
Tout d’abord pour chacune des années composant l’historique retenu, les fréquences cumulées de la fonction de distributions des classes de risque sont calculées. L’objectif est de rendre les classes comparables à travers la période considérée.
Les valeurs obtenues sont les suivantes :
Les nouvelles classes sont maintenant réaffectées à l’ensemble du portefeuille comme le montre le tableau qui suit. Le portefeuille n’est désormais plus constitué de deux classes de risque A et B mais de quatre classes (allant de 1 à 4) réassignées à chacune des expositions en fonction de sa classe de risque pour chacune des années de la période considérée (25%, 30%, 35% et 100%).
L’AUC est ensuite calculée à partir de ces nouvelles classes 07.
Les résultats obtenus à partir de notre modèle de probabilité de défaut sont les suivants.
L’hypothèse nulle du test selon laquelle il n’existe pas de différence statistiquement significative entre l’AUC calculée sur la période de développement et celle calculée sur la période de backtesting, n’est pas rejetée. En effet, la p-value obtenue est supérieure à 5%. On constate un léger gain de pouvoir discriminant sur la période backtestée par rapport à la période de développement.
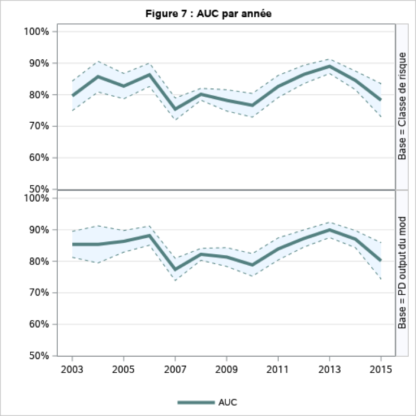
On observe cependant, une perte de pouvoir discriminant depuis 2013, même si ce dernier se maintient toujours à un seuil que nous jugeons acceptable puisque situé au-dessus de 70%. Veuillez noter qu’il n’existe pas de différence significative entre l’AUC calculé à partir des classes de risque regroupées et celui calculé à partir du score sous-jacent.
La méthode de construction de la statistique nous amène à un questionnement notamment lors de la première étape, où la notation utilisée pour le calcul de l’AUC est remplacée par la distribution cumulée des classes de risque.
En effet, le fait de remplacer cette valeur par la distribution cumulée est en soit cohérent avec la construction de l’AUC qui repose sur la statistique de Mann-Whitney, où seul l’ordre des observations est important. Cependant, un biais pourrait être introduit par cette méthode car cette nouvelle notation vient définir le nombre de points sur la courbe ROC. Par conséquent, si les distributions cumulées se retrouvent aux mêmes points sur deux périodes distinctes le nombre global de points pour la construction de la courbe ROC diminue, et par définition, l’AUC sera plus faible.
En effet, si l’on reprend l’exemple précédent (voir l’encadré ci-dessus), nous sommes en présence de quatre classes réassignées. Nous disposons donc de quatre points sur la courbe ROC. Si maintenant, la fréquence cumulée de la classe de risque B pour l’année 3 n’est plus 35% mais 25%, nous n’aurions plus quatre classes réassignées mais seulement trois (25%, 30%, et 100%) et donc trois points pour construire la courbe ROC. Dans ce cas, nous perdons en précision et donc la valeur de l’AUC sera d’autant plus faible.
Par conséquent, cette diminution du nombre de points de la courbe ROC, causée par la méthodologie de réassignation des classes de risque, pourrait engendrer un rejet de l’hypothèse nulle, l’écart entre les courbes ROC des deux périodes pouvant devenir statistiquement significatif.
2. Tests généraux retenus en interne
L’exercice de backtesting interne doit s’assurer de la qualité du pouvoir discriminant du modèle de risque. Une mesure de performance d’un système de classification binaire est utilisée afin de catégoriser les expositions en deux groupes. En général, une représentation visuelle est réalisée, à laquelle on ajoute une valeur d’agrégation.
Les mesures que l’on retrouve le plus souvent, à cause de leurs propriétés statistiques, sont les suivantes :
- la courbe de Lorenz ou « Cumulative Accuracy Profile » (CAP), accompagnée de la valeur d’agrégation appelée le coefficient de Gini ou « Accuracy Ratio » (AR) . Elle représente le taux de vrais positifs en fonction du taux d’expositions considérées et ce, pour différents seuils, jusqu’à comptabiliser la population entière ;
- la courbe « Receiver Operating Characteristic » (ROC) accompagnée de la valeur d’agrégation appelée l’ « Area Under the Curve » (AUC) ou « Pietra coefficient ». Elle représente le taux de vrais positifs en fonction du taux de faux positifs et ce, comme pour la courbe de Lorenz, pour différents seuils, jusqu’à comptabiliser la population entière.
Veuillez noter que tous ces indicateurs sont linéairement liés08.
Cependant, il existe aussi d’autres mesures qui pourraient également être utilisée par la validation interne :
- le « Bayesien error rate » ;
- L’entropie conditionnelle accompagnée de la valeur d’agrégation « Kullback-Leibler distance » ou « CIER » ou encore « Information Value » ;
- Le Tau de Kendall et D de Somers ;
- le « Brier score » values.
L’ensemble des mesures citées ci-dessus sont explicitées de façon détaillée dans la référence (1).
Le backtesting interne se fonde souvent sur la valeur du pouvoir discriminant ainsi que sur sa variation. En effet, habituellement un seuil interne est défini et si le pouvoir discriminant est au-dessus de ce seuil, l’entité considère que le pouvoir discriminant du modèle est toujours adéquat exception faite en cas d’une baisse significative de ce dernier. La BCE, quant à elle, a fait le choix de se focaliser uniquement sur le fait qu’il y ait ou non une baisse du pouvoir discriminant sur la période backtestée par rapport à la période de développement, et ce quelque soit le seuil défini par la validation interne. Cette approche est tout à fait justifiable par le fait qu’il serait délicat d’imposer un seuil qui convienne à tous les types de modèles.
Une divergence dans les conclusions des tests pourrait exister si le seuil minimal défini par l’établissement est plus faible que la borne inférieure de l’intervalle de confiance défini par la mesure de la BCE, ou si la grille de lecture des p-values choisie par l’établissement, diffère de celle de la BCE. Cette dernière s’intéresse uniquement à la variation de l’AUC et non pas à sa valeur en elle-même. En effet, dans le cas de la mesure de la BCE, une perte du pouvoir discriminant significative serait à considérer et, ce même si le seuil défini par le backtesting interne n’est pas encore atteint.
Conclusion
Rappelons que cet article a pour objectif de comprendre le fonctionnement et la sensibilité des tests demandés par la BCE, ainsi que leur complémentarité avec les tests généralement retenus pour les exercices de backtesting internes. Pour ce faire, nous avons opté pour l’illustration de cette problématique, à travers l’exemple d’un modèle de probabilité de défaut sur un portefeuille retail avec un faible taux de défaut.
Les trois composantes principales décrivant généralement l’exercice de backtesting règlementaire ont été utilisées, à savoir : la stabilité de la population, le conservatisme de l’estimateur et enfin le pouvoir discriminant du modèle. Pour chacun des volets, nous avons présenté la ou les mesures demandées par la BCE ainsi que les tests habituellement utilisés en interne, afin de mettre en évidence leur complémentarité.
A travers l’ensemble de ces résultats, on constate que sur la période de validation, la population est plutôt stable et que le modèle conserve sa capacité prédictive et son pouvoir discriminant.
Les tests de stabilité retenus par la BCE nous apportent de l’information complémentaire par rapport aux tests habituellement utilisées en interne. En effet, de façon générale, le backtesting interne s’intéresse aux différences de distributions observées lors de la dernière année, tandis que les mesures requises par la BCE portent davantage sur la nature des migrations réalisées. De plus, deux dimensions sont abordées dans les mesures requises par la BCE, à savoir, la pondération en nombre de contrats et en encours tandis qu’habituellement on se focalise sur la distribution de la population en termes de contrat, comme le requière le calibrage des estimateurs bâlois.
Le test de Jeffreys retenu par la BCE nous apporte de l’information additionnelle sur le taux de défaut ponctuel de la dernière année, ainsi que sur le conservatisme de l’estimateur. En effet, dépendamment de la stratégie adoptée par le backtesting interne et la philosophie du modèle considéré, les tests habituellement utilisés portent davantage sur la précision de l’estimateur. Le test de Jeffreys est généralement préconisé pour les modèles de type PiT de par le fait, qu’ils présentent des taux de défauts plus stables au cours du temps.
Enfin, concernant le pouvoir discriminant, en interne on s’intéresse habituellement à la valeur de ce dernier, comparée à un seuil fixé tandis que la BCE a choisi de s’intéresser à sa variation. En effet, en cas de baisse jugée suffisamment significative par le test, la mesure renvoi un signal et ce, quelle que soit la valeur du seuil fixé en interne.
L’exercice n’est qu’un exemple et n’a pas vocation à mettre en exergue toutes les configurations possibles de complémentarité ou de divergence entre le backtesting interne et les tests exigés par la BCE. Nous suggérons aux lecteurs, de faire cet exercice sur chacun de leurs portefeuilles et pour l’ensemble de leurs paramètres de risque.
- 1. Pour plus de détails sur ces indicateurs, veuillez vous référer à la section 2.5.5.1. de (2). [↩]
- 2. Pour plus de détails sur ces indicateurs, veuillez vous référer à la section 2.5.5.2. de (2). [↩]
- 3. Pour plus de détails sur ces indicateurs, veuillez vous référer à la section 2.5.5.3. de (2). [↩]
- 4. Pour plus de détails sur ce test, veuillez vous référer à la section 2.5.3.1. de (2 [↩]
- 5. Pour plus de détails sur cet ajustement, veuillez consulter la référence (6) [↩]
- 6. Pour plus de détails sur ce test, veuillez vous référer à la section 2.5.4.1. de (2). [↩]
- 7. Pour plus de détails concernant la construction des nouvelles classes, veuillez vous référer aux sections 2.5.4.1 et 3.1 de (2). [↩]
- 8. Pour plus de détails sur ces valeurs d’agrégation, veuillez vous référer à (7). [↩]



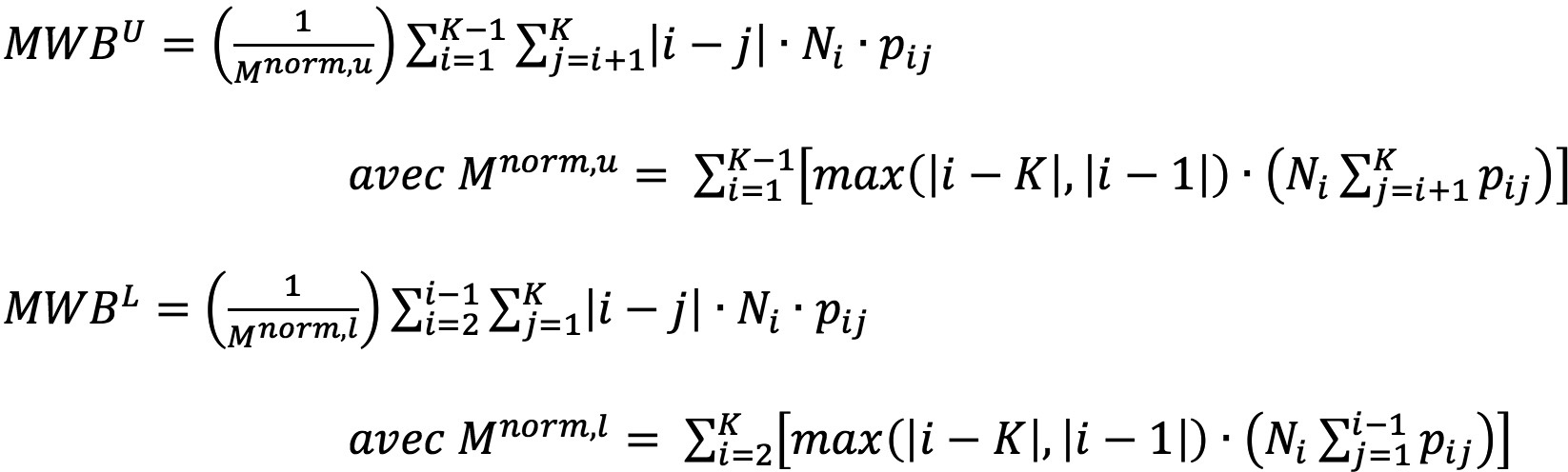


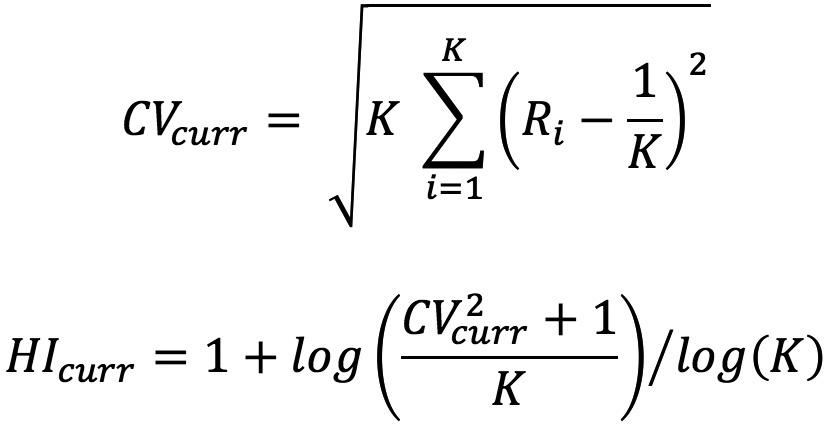






Sorry, the comment form is closed at this time.